שימת עין 🔗
על דבר ידיעת הרב רבי שניאור זלמן מלאדי בחכמת ההנדסה, התכונה והטבע
(מילואים) 🔗
השחר אשר החל להפציע אורו בארצות מערב אירופה במאה השלישית לאלף שאנו עומדים בו, ויער נרדמים משנתם לשוב ולהשיב לחיים חדשים את החכמות והמדעים, אשר שכבו במחשכים כמתי עולם כל ימי דורות הבינים, השחר היפה הזה, אשר הלך הלוך וחזק עד שנתמלאו הארצות ההן כלן אורה, הבקיע לאחרונה בסוף המאה החמישית לאלף הזה גם אל ארצות מאפליה, אל מדינות פולין וליטא, וישלח את קרני הודו גם אל משכנות היהודים, אשר יחד עם יתר יושביהן שכנו עד כה בערפל. מלבד החוקרים והפילוסוף הגדול ר' שלמה מימון (נולד בתחלת המאה הששית), הנודע לתהלה גם בספרות העמים, הננו פוגשים עוד לפניו בפולין את הרב ר' ישראל מזאמושץ (בעל “נצח ישראל” וספרים אחרים) ואת הרב ר' שלמה מהעלם (בעל “מרכבות המשנה”), ובאותו הזמן בליטא את הרב ר' ברוך משקלוב (מעתיק ספר “אקלידוס” וספרים אחרים), אשר כתבו ספרים שונים בחכמת ההנדסה ותכונת השמים. רוח החכמה והדעת אשר החל לפעם בלב בחירי העם, צרר בכנפיו גם את גדולי מנהיגיו ומנהליו, אשר רק התורה לבדה היתה אומנותם, והננו רואים בעת ההיא את שני אנשי השם אשר היו לאות ולמופת בישראל, ואשר רחקו בדעותיהם איש מאחיו מרחק רב, את הגר"א מווילנא ואת הרב מלאדי, עוסקים גם בחכמת החשבון וההנדסה; הראשון כותב במקצוע זה ספר מיוחד (“איל משולש”), והשני משתמש ביסודות החכמות האלה לצורך משאו ומתנו בהלכה. מאין שאבו החכמים האלה את חכמתם, בעת אשר ספרי המדע מעטים היו בארצות מגוריהם וכתובים בשפה זרה, בשפת רומי אשר היתה לנחלה אך לכהני הנוצרים ולאצילי העם? קרוב בעיני לשער כי כלם רכשו להם את ראשית ידיעותיהם מן הספרים המעטים שהיו לפניהם בשפת עבר 1), כמו “צורת הארץ” להנשיא, “יסוד עולם” להישראלי (שהיה בכתב-יד לפני בעל “נצח ישראל”), פירוש קידוש החודש לר' עובדיה, “נחמד ונעים” לר' דוד גנז ו"תכונת-השמים" לר' רפאל הנובר, אשר מהם יכלו לקנות לעצמם ציור נכון, אם מעט ואם הרבה, מבנין העולם ומהלך המאורות והככבים בכלל, ואולם יותר מכל אלה היה להם לעינים ספר ה"אלים" לר' יש"ר מקנדיה, אשר משך עליו את עיני חכמי הדורות מיד כאשר אך יצא לאור (בעל תוספות יום טוב, מביאו כבר במשנה ריש ברכות) עד זמן החכמים האחרונים. הספר הזה, אשר בחלקו הנקרא בשם “סוד היסוד”, יכיל את חכמת המשולשים הפשוטים והכדוריים (כפי מצבה בזמנו), ובחלקו “חקות שמים” – סדר חשבונות התכונה, היה ביד החכמים ההם לכלי חפץ להשתמש בו גם בעיון גם במעשה, והספר הנכבד הזה אשר לא רבים יחכמו להבינו, היה בלי ספק נר גם לרגלי הרב מלאדי, אשר אנו באים לדבר פה על אודותיו, ואשר העמיק לחקור ולעיין בו, גם עמד על סוף דעתו, כאשר נראה במרוצת דברינו.
אחרי הדברים האלה נעברה נא על ספרי הרב ונלקטה את הדברים אשר יחס וקשר להם עם החכמות הלמודיות. החמר אשר יעלה בידינו לא רב יהיה, כי הרב בכל אהבתו ובקשתו את החכמות המדוקדקות (עקסאקטע וויססענשאפטען) לא חבר ספר מיוחד על אודות הענינים האלה, כאשר עשה הגאון, אך הם היו לו לכלים ומכשירים לחקירותיו בחכמת התורה ובאלהות, בכל זאת יספיק לנו החמר הזה לראות עד כמה היה כחו של הרב גדול במדעים האלה.
א) בשלחן ערוך שלו (אורח חיים סימן צ"ד), אחר שיביא הרב את דברי התלמוד, שהיושבים בחו"ל צריכים להחזיר פניהם כנגד ארץ-ישראל, הוא מוסיף: “במדינות אלו שהן לצד צפון הרבה, אף על פי שהן במערבו של ארץ ישראל, לא יקבעו מקום הארון וצד תפלה, דהיינו כותל מזרח, כנגד אמצעית רוח מזרחית שלהם, אלא כנגד מזרחית דרומית קצת, כפי ערך נטיית נקודת אמצע מזרח שלהם מכנגד ירושלים (ונקודה זו היא מקום יציאת שמש לעיר זו בתקופת ניסן ותשרי האמיתית, והוא מקום פגישת גלגל משוה היום באופק עיר זו, שלכן היום והלילה שוים שם בתקופת ניסן ותשרי). ומקום זה בכל מדינות אלו הוא להלאה מנקודת נוכח הראש של ירושלים. וצריך לחשוב כמה יהיה כנגד ירושלים ברוחב שמגלגל משוה היום עד רובע עגול שמנוכח הראש שלנו עד מקום פגישת האופק שלנו במשוה היום; ואם רוחב זה שמעגול זה עד משוה היום כנגד ירושלים הוא יותר מרוחב שממשוה היום עד נוכח הראש של ירושלים, צריך לצדד קצת לדרום כפי ערך יתרון הזה, ואם הוא פחות מזה צריך לצדד לצפון קצת. ודבר זה תלוי במרחק המדינה מים המערבי כלפי המזרח, ובהרחקה מטבור הארץ כלפי צפון יותר ממרחק ירושלים וחשבון זה קל להיודעים דרכי החשבון במשולש כדורי”. עד כאן לשון הרב בתקון קצת 2. וכונתו, כי אם באחד המקומות בכדור הארץ נחפוץ לדעת נטיית הרוח המכוונת כנגד ירושלים. אז עלינו למשוך ברעיוננו עגול גדול העובר על נקודת הקדקד של המקום ההוא, ועל נקודת אמצע המזרח שלו, במקום שהאופק נחתך עם משוה היום. העיגול הגדול הזה יחתוך באחת הנקודות את עגול הצהרים העובר על ירושלים; ומובן מאליו שאם תפול הנקודה הזאת לדרומה של ירושלים (בין ירושלים ובין עגול המשוה), אז צריכים אנו להפוך פנינו לצד צפון, ואם תפול לצפונה של ירושלים, עלינו להסב פנינו כלפי דרום, או במלין אחרות: אם מרחק הנקודה הזאת מעגול המשוה הוא פחות מרחבה של ירושלים עלינו להצפין, ואם יותר – עלינו להדרים. אל הקשת הזאת שבארנוה, האחוזה בין נקודת החתך שהזכרנו ובין עגול משוה היום, יכוון הרב בדבריו שהעתקנו למעלה, ושאנו מוסיפים בהם מלים אחדות לעשותם מובנים יותר, וזה לשונו: “וצריך לחשוב כמה יהיה כנגד ירושלים, ברוחב מגלגל משוה היום עד רובע העיגול [היוצא מנקודה] שמנוכח הראש שלנו [יורד] עד מקום פגישת האופק שלנו במשוה היום וכו'”. והוא מסיים דבריו: “ואם רוחב זה וכו' הוא יותר מרוחב שממשוה היום עד נוכח הראש של ירושלים (או בקיצור יותר: מרחבה של ירושלים), צריך לצדד קצת לדרום כו', ואם הוא פחות מזה צריך לצדד לצפון וכו'”. על ידי ידיעת הקשת הזאת, אשר נקל מאד למצאה בחשבון 3), נוכל אפוא להכריע לאיזה צד עלינו לנטות, כדי לכוון כנגד ירושלים.
ההתרה הנכונה שנתן הרב לשאלה הזאת, והלשון הקצר ששנה בו את משנתו, יוכיחו לנו, כי הידיעות בחכמות הלמודיות, שקנה לו מפי ספרים, נבלעו יפה בדמיו ונתבשלו היטב במוחו, עד שעלתה בידו להביע את חפצו בשפה קצרה ונמרצה.
והנה בעיקר הדבר כבר קדמהו הרב ר' ישראל זמושץ, שהתיר גםהוא את השאלה הזאת בספרו “נצח ישראל”, (פרנקפורט דאדר שנת תק"א,דף נ"ב) באותה הדרך עצמה שדרך בה הרב מלאדי, ואפשר היה לחשוב כימשם שאב את דבריו. אולם יש לנו ידים מוכיחות להחליט, כי בכל אופן עשה הרב את חשבונותיו מדעת עצמו, ולא נעזר בדברי בעל “נצח ישראל”.
דרך ההתרה שהלכו בה שני החכמים האלה תורנו אך בכלל, אם במקום פלוני או פלוני עלינו להצפין או להדרים, אבל לא תתן לנו את שיעור זוית הנטיה כמה היא, ואת השיעור הזה נתן לנו הרב בסדר תפלה שלו (דיני תפלה) וז"ל: “ומה שנהגו לעמוד כלפי מזרח נתפשט המנהג מימי קדם כשהיתה הגולה בצרפת וסמוכות שלה, אבל במדינות אלו הצפוניות ביותר צריך לעמוד כנגד קרן דרומית מזרחית, ולא כנגד הקרן ממש, אלא משוך מן הקרן מעט כלפי דרום, בענין שאם תחלק רובע העיגול שמאמצע הדרום לאמצע המזרח לשלשה שלישים, יהיו פניו מכוונים כנגד רוחק ערך שליש אחד מאמצע הדרום וערך שני שלישים מאמצע המזרח”. מדבריו אלו נראה, שהתיר הרב בעצמו את השאלה הזאת על כל פנים על שני מקומות ידועים, בארץ צרפת ורוסיא, ומצא שבראשון מהם הנטיה כנגד ירושלים מכוונת עם נקודת אמצע המזרח, ובשני היא משוכה מאמצע המזרח כלפי דרום בשיעור ששים מעלות. אכן פה יִוָלֵד לנו בסקירה הראשונה קושי גדול, כי באמת לא ימצא בכל גבול צרפת אף מקום אחד, שהמתפלל כנגד ירושלים צריך לעמוד מכוון כנגד אמצע המזרח, וכן לא ימצא בכל רחבי ארץ רוסיא אף מקום אחד שזוית נטייתו תהיה מכוונת עם השיעור שקצב הרב 4. אולם הקושי הזה יסור מאליו אם נשים לב, כי לפי מצב החכמה וההשכלה בימיו, לא היה הרב יכול לדעת אורך ורוחב המקומות שהיה ברצונו לייסד חשבונותיו עליהם. מצד אחד לא היו מפות הארץ בימים ההם מצויות ביד כל איש, ומצד השני לא היו המפות ההן מדויקות די צרכן, ובפרט בענין ארכי המקומות שידיעתם היתה קשה מאד בעת ההיא5, ויותר מזה היה הדבר קשה בארץ רוסיא, אשר מעטו אז בתוכה הערים אשר ישבו בהן חכמים מומחים, שהיתה היכולת בידם לקצוב את מקומותיהם אפילו באותו הדיוק שהיה אפשרי להם בימיהם. ואין ספק בדבר, כי בבוא הרב לערוך חשבונותיו בקש לו ידיעת ארכי המקומות ורחבם, על פי רשימות שמצא בספרים שהיו לפניו. אחת מרשימות כאלה נמצאת בסוף ספר חקות שמים לר' יש"ר מקנדיאה, והוא חלק מספר אלים, שהביא הרב בעצמו במקום אחר, אשר נזכיר עוד מעט במרוצת דברינו. כל המספרים אשר ברשימה הזאת נוטים כלם מן האמת אם מעט ואם הרבה, ובפרט בארכי המקומות שההבדל מגיע בהם לפעמים לט"ו מעלות ויותר. הבדל האורך למשל בין ירושלים וליסבון עולה שם קרוב לס"א מעלות, בזמן שההבדל האמתי הוא רק '20 440, אמנם נפלא הדבר, כי לפי המספרים שברשימה הזאת, ימצאו באמת מקומות שונים בדרומית מערבית של ארץ צרפת, שיושביהם צריכים לפנות בתפלתם מכוון כנגד אמצע המזרח. בעיר באיונה למשל, שרחבה לפי הרשימה הזאת '50 420 (בזמן שרחבה באמת"29 '29 430 ) ורחוקה מירושלים למערב '30 480 (בזמן שההבדל באורך עולה באמת רק "12 '40 360), זוית הנטיה אינה מגיעה כי אם חלק אחד מי"ב במעלה כלפי דרום. וכן בערים אחרות בצרפת לא תעלה זוית הנטיה כי אם למעלות אחדות, שיעור שאינו מורגש כלל לעין, ולכן בצדק היה יכול הרב להוציא משפט, כי מנהגנו לעמוד כנגד המזרח בא אלינו מחכמי צרפת 6. אבל עוד יותר מזה נראה, כי שיעור הנטיה שנתן הרב למדינת רוסיא גם הוא מכוון רק עם לוחות בעל האלים. בלוחות האלה הכוללים אורך ורוחב קכ"ו מקומות שונים, תזכר רק עיר אחת מתחום מושב היהודים ברוסיא, והיא “וילנה במדינת ליטה ראש”, ורחבה קצוב שם 53.5 מעלות, בזמן אשר באמת רחבה הוא '41 540), והבדל האורך בינה ובין ירושלים הוא 140 (בעת אשר באמת יעלה ההבדל הזה רק "7 '54 90). אם על פי השיעורים האלה נחשוב את שיעור זוית הנטיה אשר לעיר ווילנא, אז נמצאה בדיוק '13 300 מאמצע הדרום, והוא מכוון לגמרי עם דברי הרב. הנה כי כן לא לבד שנסתלק כלה הקושי שמצאנו בדברי הרב, אלא אף זו, שנודע לנו בדקדוק הספר שסמך עליו, והוא ספר “אלים” אשר היה מבחר שעשועיו 7.
לאיש היודע את דרכי החשבונות במשולשים כדוריים, תהיה השאלה הזאת קלה ופשוטה
מאד. כי במשולש הכדורי הנולד על ידי שלש הנקודות, שהן: נקודת הציר הצפוני
נקודת הקדקד של ירושלים ונקודת הקדקד של המקום שזוית נטייתו מתבקשת, אנו
יודעים את מדת שתי הצלעות ואת מדת הזוית הסגורה ביניהן, נקל אפוא למצא את
מדת שתי הזויות האחרות. והזוית שהצלע השלישית, והוא רובע העגול היוצא
מנקודת הקדקד של מקומנו ועובר על נקודת הקדקד של ירושלים עושה עם הצלע
השנית, שהוא אופן הצהרים שלנו, היא היא זוית הנטיה המתבקשת. השאלה הזאת
נתרת יפה על ידי לוחות המגבילים על פי התמונה הנקראת על שם החכם האנגלי
נעפער ((Napier 8,
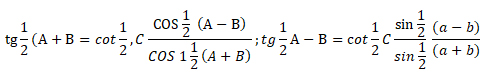 (מסיבות טכניות המשוואה שבהערה 8 מופיעה בגוף הטקסט - הערת פרויקט בן יהודה)
(מסיבות טכניות המשוואה שבהערה 8 מופיעה בגוף הטקסט - הערת פרויקט בן יהודה)
וכבר התירה בדרך כזו הרב בעל אמונת חכמים, במאמרו שכתב בלשון איטלקי 9. קשה לנו לדעת אם ראו שני החכמים האלה את דברי בעל אמונת חכמים, אבל גם אם ראום, אי אפשר היה להם להשתמש בהתרתו, מפני שהיתה כתובה בשפה זרה להם. אבל אם רוצים אנו להכיר בדבר הזה את ערך הרב, עלינו לשים אל לב כי לא כימים האלה היו הימים הראשונים אשר היו לפנינו. בימינו אלה ספרי חכמה ומדע גלויים לפני כל איש היודע אך שפה אחת מלשונות אירופה, וידיעת העקרים הראשונים מצורת העולם (קוסמוגרפיה) ודרכי החשבונות במשולשים כדוריים אינם עוד נחלת יחידי סגולה, אבל לא כן היה מצב הדברים בימים ההם, והתרת שאלה כזאת, ובפרט בין יהודי רוסיא, לא היתה יכולה להעשות בלתי על ידי בני-עליה המעטים מאד. ובאמת שלשת החכמים האלה, אשר הכרנום עתה: בעל “אמונת חכמים” בעל “נצח ישראל” ובעל ה"תניא", אינם הראשונים אשר התעסקו בשאלה הזאת, וכבר נגעו בה שני חכמים לפניהם, אבל לא הצליחו במלאכתם. החכם הקראי ר' אליהו בשיצי, שכתב את ספרו “אדרת אליהו” (שנת ר"ן לאלף שלנו), שהיתה לו ידיעה מסוימת בעקרי חכמת התכונה, ואשר הרחיב מאד לדבר בספרו בענין קידוש החודש (אם אמנם לא נקה גם שם משגיאות), היה אחד מן הראשונים שנגעו בשאלה הזאת, וגזר אומר, כי ראוי לבנות הכותל ההוא (שארון הקודש נתון בו) מכוון כנגד המקדש לפי שרשי התכונה והתשבורת בלי שום טעות" (ענין תפלה פ"ג). אחרי דברים כאלה יוכל הקורא לחשוב בצדק כי ימצא פה התרה מדוקדקת, מיוסדת על אדני ההנדסה והתכונה, ומה יתפלא לראות, כי בכל אריכות דבריו על עיגול האופק, אופן הצהרים ונקודת אמצע המזרח ויתר רוחות העולם, על אורך המקומות ורחבם, ואחרי צללו במים אדירים לא העלה בידו כלום. המחבר מצייר לו דמות עיגול על שטח אופקי ישר, מציין בו בקוים ישרים את עיגול המשוה ואופן הצהרים, או ארבע רוחות השמים, מסמן לו על ידי שתי נקודות מקומה של ירושלים ואת המקום שעליו נבנה בית הכנסת, לפי ארכם ורחבם שהוא לוקח מתוך הלוחות אשר בספרים, מצרף את שתי הנקודות האלה בקו ישר, ומוצא בדרך רשימה הזאת כמה הקו הזה נטוי על הקוים המצרפים את המזרח עם המערב ואת הצפון עם הדרום, ולא ישים המחבר אל לב, כי אין לנו כל עסק פה עם שטח ישר כי אם עם שטח כדורי, וכי אין השאלה נתרת בדקדוק כי אם על ידי חשבון המשולשים הכדוריים. ולפי דרכו של בעל האדרת יצא לנו, כי כל יושבי המקומות שרחבם הצפוני גדול מרוחב ירושלים, צריכים להחזיר פניהם לדרום, בעת אשר במקצת המקומות בספרד ופורטוגליה צריכים באמת להפוך פניהם לצפון. כדבר הזה קרה גם את בעל ה"לבושים", אשר חרץ משפט גם הוא, שכל הארצות הצפוניות לארץ ישראל צריכים לנטות כלפי דרום, ולא העיר כי יש מן הארצות הצפוניות שצריכות לפנות כלפי צפון, וכאשר כבר השיבו עליו שני החכמים בעל “אמונת חכמים” ובעל "נצח ישראל 10 בספריהם, (אבל הרב בשלחן ערוך שלו אינו מדקדק כל כך עם הלבוש, והוא מסכים עמו בעיקר הדבר, שאנו מחזירים פנינו לא לצד מזרח אלא נגד ירושלים, ואינו מקפיד עמו כחוט השערה על שלא שם לבו להעיר, שיש מקומות שהם צפוניים שאנו זקוקים בם להפוך פנינו לצפון).
מכל הדברים האלה נראה, כי הרב בעל “נצח ישראל” באמרו כי “דבריו הם עם המעמיקים בחכמה” לא היה מתפאר בשקר, וכי בצדק יזכיר החכם מימון בספר תולדותיו (חלק ב' עמוד 170), במנותו את שבחיו של בעל “נצח ישראל”, גם את התרתו הנכונה לשאלה הנזכרת, ועל אחת כמה וכמה שיש לנו להזכיר בדבר הזה לשבח את הרב מלאדי, אשר סוף סוף לא היתה חכמת השיעור אומנותו.
ב) בסדר התפלה שלו כתב הרב מאמר מיוחד הנקוב בשם “הכנסת שבת”, ונראה שהוא הוא המאמר הנזכר בהקדמת בניו לשלחן-ערוך בשם “קונטרס בין שמשות”, אשר בו העמיק במשא ומתן של הלכה על דבר בין השמשות וגבול היום והלילה.
המאמר הזה נכבד בערכו מצד חלק ההלכה שבו, כי ערב הרב את לבו לסור משיטת רבנו תם, שנתפשטה ונתקבלה בין הפוסקים, ואשר נמשך אחריה גם הוא בעצמו בשו"ע או"ח (סימן רס"א), וישב להחזיק בשיטת הרמב"ם והגאונים, אשר כפי שהראה מחוורת יתר בדברי התלמוד ומסכמת יותר עם המציאות 11. בדבר הזה נפגש הרב יחד עם בר פלוגתיה הגר"א בביאוריו לשו"ע או"ח )סימן רס"א) ושניהם נתכוונו בענין הזה לדבר אחד, כי השכל הישר וידיעת עקרי חכמת התכונה, היו נר לרגלי שניהם. אכן לרגל חקירתנו נכבד לנו לראות גם פה, כי ידע הרב להשתמש בחשבונות המשולשים הכדוריים, אשר למד מספר “אלים” שיזכירנו בדבריו, ולהוציא מהם תועלת אל השאלה שהיה דן עליה. הרב אינו מברר לנו את חשבונותיו, אבל דרכו מבואר מעצמו וגלוי לכל מבין. הוא לוקח לו ליסוד את דברי התלמוד (שבת ל"ד), ששיעור בין השמשות הוא שלשה רבעי מיל, שהוא שוה בזמן לי"ח מינוטין, ומוסיף עליהם שני מינוטין, שהוא שיעור בין השמשות של רבי יוסי המתחיל אחר בין השמשות של רבי יהודה, ומוצא שסוף בין השמשות הוא כמו שליש שעה אחר שקיעת החמה “האמיתית”, או כ"ד מינוטין אחר השקיעה “הנראית 12 השיעור הזה הוא בארץ ישראל ובתקופת ניסן ותשרי שהיום והלילה שוים 13, אבל במדינות אלו הוא עולה בניסן ותשרי לחצי שעה בקירוב אחר שקיעת החמה האמיתית, או ל”ד מינוטין לאחר השקיעה הנראית 14. ודבריו נכונים וישרים, כי משיעור שליש שעה, שבין השמשות נמשך לדעת בעלי התלמוד בארץ ישראל, נמצא בחשבון שחשבו את תחילת החשכה בזמן שירדה השמש 4.25 מעלות אל תחת האופק. את שיעור הקשת הזאת תעבור השמש במקומותינו (בעיר ווילנא למשל שרחבה, לדעת בעל ספר אלים, שאחריה נמשך הרב, נ"ג מעלות וחצי) בשיעור 28,6 מינוטין לאחר השקיעה, מכוון בקירוב גדול עם דברי הרב.
סבת הדבר שקצב הרב את שיעור בין השמשות רק לתקופת ניסן ותשרי ולא לתקופת טבת ותמוז, ראה שבאופן הראשון היה יכול להשתמש בהתרת משולש כדורי נצב, שהיא קלה ביותר 15, מה שאין כן באופן השני, שאנו זקוקים להתרת שני משולשים שאחד מהם עקום, שלא היה בידי הרב להתירו כי אם אחרי הפרידו אותו לשני משולשים נצבים, ונמצא טורח העבודה לכל הפחות פי שלש 16), אבל מצד אחר נראה, כי השתדל הרב להתיר את השאלה גם חוץ לזמן שווי היום והלילה. והדבר שהביאו לידי כך הוא מה שכתב ר' יש"ר מקנדיאה (חוקות שמים" שאלה ל"ה, “מעין חתום” תמר ס"ד), שהקצר שבנשפים הוא בזמן שהשמש היא “בנקודה שבין מאזנים לגדי”, ולכן נסה הרב למצא את זמן בין השמשות הקצר ושיעורו, ולפי חשבונו יצא לו “שבמרחשוון של חדשי החמה פוחת מעט מתשרי שנראין אז ג' ככבים בכחצי שעה אחר שקיעה הנראית, ובטבת עודף מעט על תשרי, ובאדר חוזר ופוחת מעט כבמרחשוון, ובניסן חוזר להיות בשוה עם תשרי, עיין בספר “אילים” במעין חתום” עכ"ל, וכמו שהבאנו למעלה בהערה, אבל במחילת כבוד הרב לא עלה לו חשבונו יפה. בין השמשות הקצר העיוני הוא באמת מיד כארבעה וחצי יום אחר תקופת תשרי, ולא יקטן מבין השמשות הבינוני רק כשתי סיקונדין, וכארבעה וחצי יום אחרי כן כבר הוא שב להיות שוה עם בין השמשות הבינוני שבתקופת תשרי, ומוסיף והולך עד תקופת טבת. דקדקתי בדברי ואמרתי: “בין השמשות העיוני”, כי באמת ההבדל שבין בין השמשות הקצר והבינוני אינו שיעור מורגש כלל, ואפילו היה בכחנו להבחין בין גבולות היום והלילה כחוט השערה, גם אז לא היה ההבדל עולה כי אם לשתי סיקונדין לערך, ולא לארבעה מינוטין כאשר חשב הרב; אבל במעשה נוכל לומר, שבין השמשות עומד על מדה אחת כשמונה או תשעה ימים אחר תקופת תשרי, ומשם הוא מתחיל להוסיף עד תקופת טבת כאשר נראה עוד מעט. מאין יצא להרב השיעור הזה? קשה להחליט דבר ברור, אך בדרך השערה אחשוב, כי מפני שהיה קשה לו להרב לדקדק בשיעורים קטנים מאד, לכן בראותו שאי אפשר היה לו למצא כל הבדל מסויים בשיעור בין השמשות הבינוני והקצר, ובדעתו על פי דברי בעל ספר “אלים”, שהבדל כזה מוכרח להמצא, תלה את הדבר בחסרון לוחות הבקעים שהיו לפניו בספר אלים, שבאמת לא היו מסוגלים כלל לחשבונות מדוקדקים כאלה, וישם פניו לבחון הדברים בנשף התוכנים, הגומר בשעה שהשמש נמצאת כשמונה עשרה מעלות מתחת לאופק, כי בנשף הזה יעלה באמת ההבדל קרוב לארבעה מינוטין 17 ודן גזרה שוה מעצמו שאף בבית השמשות הקצר הדבר כן, וכי זה שלא יכול למצאו היה מפני חסרון הדיוק שבלוחותיו.
נשאר לי עוד לדבר על ענין ההבדל שבין השקיעה הנראית והאמתית שזכר הרב, שלא מצאתי לו חבר בדבר הזה, ושאינו מבורר כל צרכו. הננו מבדילים גם אנחנו בין האופק הנראה, שהוא השטח הנוגע לכדור הארץ במקום שהאדם עומד שם, ובין האופק האמתי, שהוא השטח המקביל לאופק הנראה ועובר דרך מרכז הארץ, ולפיהם נוכל לתאר לנו גם שתי שקיעות:שקיעה נראית ואמתית. ההבדל בין שתי השקיעות האלה מגיע באמת אצל הירח לארבעה מינוטין, אבל אצל השמש לא יעלה גם לשלשה חומשי סיקונדה (ואפילו לדעת הרב החושב את קוטר השמש לי"א אלפים פרסאות, כמו שיבא לפנינו להלן, לא יעלה ההבדל בין שתי השקיעות האלה כי אם לעשר סיקונדין) 18 אבל מסגנון לשון הרב נראה, כי השׁקיעה הנראית היא אצלו ברגע שהשמש מתעלמת תחת האופק הנראה (אבל מפני שׁאין שׁטח הארץ ישר לגמרי, הוא מצוה לעיין על השׁקיעה בראשי האילנות או הגגוֹת הגבוהים), אולם השקיעה האמתית אצלו היא ברגע שאור השמשׁ מסתלק מן ההרים הגבוהים, כי אף על פי שׁלאיש השׁוכן עליהם שׁקיעת השמשׁ הנראית שוה כמעט בדיוק לשׁקיעתה באופק האמתי, הנה לא כן הדבר לשוכנים בארץ המישור, אשר הר גבוה למזרחם, כי גם אחר ששקעה להם השמשׁ עדיין הם רואים את אורה על כתף ההר אשׁר במזרח, ונקל להוכיח בחשבון שאם יהיה גובה ההר הזה כשבע מאות מטר, אז יראה האדם היושׁב לרגליו את אור השמש עוד בשׁיעור ארבעה מינוטין אחר הסתר ממנו השׁמשׁ. ולכן חשב הרב למשפט, שׁכל זמן שהוא רואה את אור השׁמש על ההר אשרממולו עדיין יום הוא, והשקיעה האמתית היא אחרי סילוק וביאת האור מן ההרים הגבוהים. הרים כאל כידוע נמצאים בארץ ישראל, לכן ראוי לאחר שם את התחלת בין השמשות בשיעור ארבעה מינוטין או להוסיפם על השקיעה הנראית, וכדי שלא ליתן דבריו לשיעורין השוה הרב את מדותיו ומוסיף את השיעור הזה גם על כל ארצות המישור, וחושב תחילת בין השמשות ארבעה מינוטין אחר השקיעה הנראית.
מן הדברים האלה יצא לנו, שבקציבת זמני בין השמשות, המיוסדת על חשבונות המשולשים הכדוריים. אנו צריכים לצאת רק מן השקיעה הנראית, התלויה רק בכדוריות הארץ לבד, אלא שלאחר גמר כל החשבונות עלינו להוסיף ארבעה מינוטין על השקיעה הנראית ועל סוף ביה"ש, כדי להשלים את שיעור הזמן שאור השמש שוהה עוֹד בארץ ישראל על ההרים הגבוהים.
והנה לקח לו הרב ליסוד, שבארץ ישראל בימים השוים שיעור ביה"ש הוא שליש שעה
לאחר השקיעה הנראית, והוא שקיעת שפת השמש העליונה, או לפי סגנון לשון
הירושלמי (ריש ברכות) “סוף גלגל חמה”, וסוף זמן ביה"ש הוא ברגע שהקשת
היוצאת מציר הצפוני, ונוגעת בשפת השמש העליונה, עושה עם אופן הצהרים זוית
בת 950. אם נעמיד המחיר הזה תחת T+t בתמונה (II) אשר בחתימת המאמר, ונעשה
את רוחב φ שוה 320 ונשים לבנו כי במקרה זה Õ = 0 שעל ידי זה תתחלף התמונה
II למשוה זו
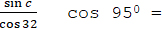 – או נמצא '15
c=40, ונמצא שבסוף ביה"ש שפת השמש העליונה הוא 4.25 מעלה מתחת לאופק.
בהנחה זו נמצא בארץ ישראל את שיעור בין השמשות הבינוני
6 os m20,
– או נמצא '15
c=40, ונמצא שבסוף ביה"ש שפת השמש העליונה הוא 4.25 מעלה מתחת לאופק.
בהנחה זו נמצא בארץ ישראל את שיעור בין השמשות הבינוני
6 os m20,
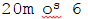 ביה"ש
הקצר 3 os m20,
ביה"ש
הקצר 3 os m20,
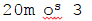 בתקופת טבת 6 21s m22.
בתקופת טבת 6 21s m22.
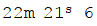 ובתקופת תמוז m23. אם נשוב ונשים
בתמונה (II) את φ = 53.50 ואת c = 4.25 אז נמצא את שיעורי ביה"ש לרוחב
1/2 53: בין השמשות הבינוני,
ובתקופת תמוז m23. אם נשוב ונשים
בתמונה (II) את φ = 53.50 ואת c = 4.25 אז נמצא את שיעורי ביה"ש לרוחב
1/2 53: בין השמשות הבינוני, 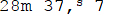 (אצל הרב חצי שׁעה בקירוב).
ביה"ש הקצר
(אצל הרב חצי שׁעה בקירוב).
ביה"ש הקצר 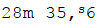 ותקוּפת טבת
ותקוּפת טבת 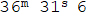 ותקוּפת תמוז
ותקוּפת תמוז 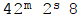
2s 8. כל השיעורים האלה נחשבים מן השקיעה “הנראית”, ומפני שאצל הרב השקיעה “האמיתית” שהוא סילוק האור מראשי ההרים הגבוהים שבא"י, מתאחרת בשיעור ארבּעה מינוטין, אנו צריכים להוסיף אותם על כל השיעורים שמצאנו.
בכל חשבונותינו אלה העלמנו עין משבירת קרני האור באויר הארץ (רעפראקציאן). וחשבנו שהשמש שוקעת בּזמן שהיא עושה עם נקודת הקדקד קשת בת 900, אף שבאמת השמש נראית לעין גם אחרי רדתה אל תחת האופק בּערך 35 דקים. בחרנו ללכת בדרך הזה מפני שהיא פשוטה יותר, ומפני ששבירת האור כמעט שאינה מעלה ולא מורדת בחקירתנו, שאנו דנים בּה רק על מרחק ביה"ש מרגע שקיעת החמה, כי כשם שאנו צריכים להוסיף '35 על 900 בחשבון שקיעת החמה, כך אנו צריכים להוסיף ולהגדיל בּמדתם את שעור c בחשׁבּוֹן בּיה"ש, ונמצא שהם מעלים ומבטלים זה את זה. לא כן הדבר בזמן שאנו רוצים למצא את רגע שקה"ח, ורגע בּיה"שׁ לפי מרחקם מחצות היום, או לפי הוראת כלי השעות, ואם אנו רוצים למצאם בּדיוק, עלינו להשׁתמשׁ גם לענין חשׁבּון שקה"ח גם לענין חשׁבון ביה"שׁ בתמונה (II), כי גם בחשׁבון שׁקה"ח אין השיעור c שׁוה o כי אם '35.
מצד אחר התמונות (II) (I) נותנות לנו את רגע שׁקיעת מרכז החמה לכן אם
נביא בחשבון את חצי הקוטר הנראה של השמש '16 ונצרף לזה מדת שבירת קרני האור
('35) אז נמצא רגע שׁקה"ח בּארץ ישׁראל בּימים השוים
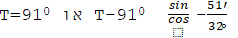 מצא שׁהשמש זורחת על הארץ עוד ארבעה
מינוטין אחר השׁקיעה היוצאת לנו בחשבון או השׁקיעה ההנדסית. על פי דרך
החשׁבון הזה נמצא את השׁיעור c שׁוה לחמשׁ מעלות בקירוב. אם נראה לדעת את
מרחק שׁיעורי בין השׁמשׁות מרגע שׁקיעת החמה ההנדסית, הנה נמצא ביה"שׁ.
מצא שׁהשמש זורחת על הארץ עוד ארבעה
מינוטין אחר השׁקיעה היוצאת לנו בחשבון או השׁקיעה ההנדסית. על פי דרך
החשׁבון הזה נמצא את השׁיעור c שׁוה לחמשׁ מעלות בקירוב. אם נראה לדעת את
מרחק שׁיעורי בין השׁמשׁות מרגע שׁקיעת החמה ההנדסית, הנה נמצא ביה"שׁ.
| הבינוני | הקצר | לתקופת טבת | לתקופת תמוז | |
|---|---|---|---|---|
| בא"י | 23m32's 8 | s,23m 32 | 26 18's 8 | 27m 7's 6 |
| ברוחב1/2 530 | 33m 42’s | ;33m 38.s,5 | 42 38’s | 49m 30’s 4 |
הננו רואים מזה כי זמני בּיה"שׁ הבּינוני הם מדוקדקים כמעט לגמרי עם השֹיעורים שׁנתן הרב: בּארץ ישׁראל 24 ובמדינתנו 34 מינוטין אחר השקיעה “הנראית”. ולפי זה היה אפשׁר לומר שׁכונת הרב בּשׁקיעה הנראית לשׁקיעה ההנדסית של מרכז החמה, בּשׁקיעה האמיתית לשׁקיעת סוף גלגל חמה לפי מראה עינינו, המתאחרת על ידי שׁבירת האור. אבל מלבד שׁסגנון לשׁונו: “סילוק האור מעל ההרים הגבוהים בּא”י", אינו יכול לסבול כל כונה אחרת זולת מה שהשׁבנוה, הנה קשׁה לומר שׁהביא הרב בחשׁבון את שׁבירת האור, שלא נמצאה אצל ישׁ"ר מקנדיאה כ"א בּמקום אחד בּדרך ארעי וסגנון סתום (“מעין חתום”, תּמר ס"ב), וכמו שׁאנו רואים שׁגם בעל תכונת השׁמים לא הזכירה כלל בּספרו. ומה גם הרב שׁלא היה צריך כלל לחשׁבון שבירת האור מפני שהוא חושׁב שׁיעורי ביה"שׁ לפי מרחקם משׁקה"ח ולא מחצות היום כמו שׁאמרנו. והדעת נותנת, שׁהשׁיעורים שׁנתן הרב לביה"ש אחר השׁקיעה הנראית, הם באמת לפי השׁקיעה הנראית, כלומר מרגע התעלם מעינינו שׁפת השׁמשׁ העליונה, שׁקרני אור השׁמש הנשׁברים באור מסתתרים מנגד עינינו, ולא אחר השׁקיעה ההנדסית, שׁאור השׁמשׁ נראה עוד על הארץ בארבעה מינוטין, כאשר אמרנו.
ג) כתב הרב בסדורו (סדר ספירת העומר) וז"ל: “וזמן התחלת עמוד השחר מח”י אייר ואילך במדינות אלו הצפוניות הוא בחצות לילה, לכך אין לספור אחר חצות אלא בלא ברכה. וזמן זה של עמוד השחר נמשך כך ע' י"ז בתמוז ועד בכלל, ולכן משהגיע חצות ליל י"ז בתמוז אסור לאכול".
משני הגבולים שנתן הרב לזמן שעמוד השחר מתחיל מחצות הלילה, שהם י"ח באייר וי"ז בתמוז, המכילים בתוכם נ"ט ימים, נוכל למצא שחשב הרב את יום י"ח באייר כ"ט יום לפני היום הארוך, והוא 23 מאי, ואת יום י"ז בתמוז כ"ט ימים לאחר היום הארוך, והוא 20 יולי (ומזה נראה שעשה הרב את חשבונו בשנת העיבור, שיום ל"ג בעומר וצום הרביעי חלים בקירוב בימי חדשי החמה הנזכרים). נטיית השמש מעיגול המשוה בשני הימים האלה, עולה 2/3 20 מעלה בקירוב, ואם נאמר שחשב הרב את התחלת עמוד השחר לאחד עם נשף הבקר של התוכנים, שהוא בזמן שהשמש הוא 180 מתחת לאופק, הנה יצא לנו שיסד את חשבונו על מקום שרחבו 1/3 51 מעלה, אכן אם נאמר שחשבון הרב מיוסד על רוחב 1/2 53 שמצא בס' “אלים”, ושהשתמש בו בבקשת הנטיה כנגד ירושלים, יצא לנו שחשב את תחילת עמוד השחר בזמן שהשמש היא תחת האופק קרוב לט"ז מעלות, (ואפשר שיצא לו השיעור הזה מדברי הרמב"ם בפירוש המשניות, ריש ברכות, החושב את שיעור עמוד השחר לשעה וחומש, כי אם נאמר שכוונת הרמב"ם על רוחב ארץ ישראל, יצא לנו שהשמש היא אז תחת האופק בערך1/2 15 מעלה 19 ואם כונתו על מקום מושבו במצרים, יצא לנו השיעור הזה לט"ז מעלות). לאיזו משני הדרכים כוון הרב, קשה להחליט בבירור.
ד) אם בסימנים הקודמים ראינו את הרב בעל התניא נמשך תמיד אחר בעל ספר “אלים”, שעשהו לרבו מובהק בחכמות הלמודיות וסמך עליו כל חשבונותיו, הנה נשוב עתה ונראה כי נוטה הוא ממנו בדבר אחד עקרי: בבנין העולם וצורתו, בעל ספר “אלים” יאמין בכל לבו בשיטת קופרניקוס, שאינו זז מחבבה אפילו שעה קלה, והרב בעל התניא עודנו מחזיק בשיטת התכונה הישנה, ואומר בסדורו (שער המילה, ד"ה: בעת ההיא): “השמש בהילוכה הוא סובב והולך וכו' וידוע בספרי התכונה בגודל גוף השמש שרחבו י”א אלפים פרסאות, ובסיבוב אחד הולך כמה רבבות אלפים פרסאות, עד אשר ערך מהלך ת"ק שנה סובב בכ"ד שעות היום, ולא ידעו טעם סיבובו במהירות עצומה כל כך, כי אם שזהו בחינת השתחוואה שלו בביטול גדול ונורא".
אכן אין לנו להתפלא כלל על המראה הזה. השקפה כזו של בעל האלים על בנין העולם, הנראית כסותרת את החוש והורסת את כל יסודי האמונה המקובלת, ששמה את האדם למרכז הבריאה כלה, השקפה כזאת לא תוכל להתבסס בלב החכם והחוקר, כי אם אחרי עיון עמוק בחזיונות רקיע השמים, ההורסים עד היסוד את כל בנין החכמים הקדמונים, ואחרי הכרה ברורה ופנימית של כל המופתים החותכים אשר העמידו את התוכנים על האמת. את כל האותות והמופתים האלה (אשר היו מספיקים למבינים גם בטרם הראה החכם פוקולט ((Foucault הצרפתי תנועת הארץ בחוש על ידי סבוב המטוטלת) לא היה יכול הרב לדעת מתוך הספרים שהיו לפניו, ומשפט היה לו להתבונן על שיטת קופרניקוס כעל השערה לבד, שלא נתבררה עוד כל צרכה. ולכן ראה את גדולת הבורא “במהירות התנועה העצומה של השמש שהיא בחינת השתחויה שלו בביטול גדול ונורא”.
אלו היה הרב חי בתנאים אחרים, ואלו היה בידו להעמיק יותר בחכמת התכונה ובחזיונותיה, כי אז קרוב מאד לשער, כי לא היה נמנע לקבל את שיטת התכונה החדשה, שנתבררה עתה בראיות שאין לחלוק עליהן, והיה מוסיף לראות בה גדולתו וגבורתו של אין-סוף בעולמות אין מספר ואין חקר, אשר כמעט “לית מחשבה תפיסא בהון כלל”. ומה נשגבו דברי החכם יש"ר בהקדמתו לס' “גבורת ה'”, בדברו על השיטה הזאת לאמר: “והייתי טופף ועופף מהשמחה על שהכרתי תוספת גדולת בוראי ית”ש, והוסיף לי שמחה ואורה, קול בשורה שהתחילו בזמננו לחשוב מחשובי החוקרים שכל העולם הוא כעששית, והנר הדולק בו הוא הגוף השמשי הזה העומד באמצעה ואורו מתפשט עד גלגל שבתי, שהוא ההיקף האחרון של זה העולם (כי שבתי היה בזמנו כוכב הלכת האחרון במערכת השמש, זאָננענסיסטעם), וכל שאר כוכבי לכת, ישנים גם חדשים, עם הרבה שאינם נראים הם בתוך העששית הזאת ונהנים מאורו. ואולם הככבים שבגלגל הח' (כלומר: הכוכבים הקיימים) יחשבו, שהם נרחקים מהיקף שבתי (כלומר מקוטר מערכת השמש), שעור גדול ורב יותר ממה שחשבו קופרניקוס, ולכן יראו כ"כ קטנים, הגם שכל אחד מהם הוא כזה העולם או יותר, (כלומר ממערכת ככבי הלכת של השמש), והאור שנראה בהם הוא מאור השמש שבכל אחד ואחד מאותם עששיות או עולמות. ומי יודע על איזה אופן יהיו, אִם להם ארץ וישוב ובריות דומות לנו".
הגיונות רמים ונעלים כאלה הביע בעל “גבורות ה'”, בעת אשר השיטה החדשה, אשר כמעט לא מלאו לה כי אם שמונים שנה ליצירתה, לא מצאה לה עוד מסלות בלבב החוקרים, בעת אשר דעת קופרניקוס היתה נחשבת לכפירה ולמינות, שמכים ועונשים עליה בכל חומר מדת הדין 20. ומה היה הרב יש"ר אומר, אלו חי בימינו, בעת אשר הענקים הגדולים: המצופיות והמחזיות, שהגיעו אל תכלית שלמותן, פתחו לפנינו שערי שמים, וגלו לנו כמה מאות אלפים כוכבי אור, שכל אחד מהם הוא מערכה שלמה של עולמות רבים, ובעת אשר מלאכת הפוטוגרפיה הפליאה לעשות ותעמק להבקיע יותר ויותר אל תוך מרחבי אין-קץ, ותוסף לגלות לנו עוד אלפי רבבות עולמות שנבראו ושעומדים להבראות, אשר לא שערום כל בעלי דמיון וחוזי חזיונות? בלי ספק היה “טופף ועופף” עוד יותר מרוב שמחה על תוספת גדולת בוראו, ובחילה ורעדה היה מתענג ומתפנק על בחינת אין-סוף של התגלות האלהית בבריאה.
-————-
אם מכל הדברים שדברנו עד כה נראה, כי היה להרב יד ושם בחשבון המשולשים הכדוריים וביסודי חכמת התכונה, וכי ידע למצוא בהם חפץ בסדר חשבנותיו, הנה לעומת זה נראה כי מעטה היתה ידיעתו בחכמת הטבע, אשר כבר עלתה בימיו למדרגה נכבדה. סבת הדבר הזה אני תולה בחסרון ספרים בשפת עבר על אודות החכמה הזאת. נפש הרב היתה מטבעה מוכשרת להתבוננות ואוהבת את העיון, וכמעט שראה את אחד מחזיונות הטבע, עשה עליו הדבר רושם ומיד העמיק להתחקות על שרשיו, ולהוציא ממנו תולדות לצורך עיקר עיונו-למחקריו באלהות. אבל גם העיון העמוק אינו מספיק כלל לידיעת חכמת הטבע שאינה נקנית אלא על ידי נסיונות הרבה ועמל חוקרי דור ודור. ואם במקום שסבת החזיון קרובה אל השכל ואינה מסובכת ביותר, אין הדבר נמנע שיעמוד עליה איש שדעתו רחבה, הנה לא כן הדבר במקום שסבת החזיון היא עמוקה ומכוסה ביותר, כי אז הנקל הוא גם לאדם גדול לשגות ברואה, ומי שגדול מחבירו שגגתו גדולה ממנו. את הדברים האלה נראה באשר יבא לפנינו.
ה) בספר “תורה אור” (סדר מקץ) יאמר הרב: “והענין שהארת אור הנר הוא על ידי שיש אויר סביב האור, מה שאין כן בלא אויר יכבה ולא יאיר כלל, ולכן אין כופין כלי על גבי הנר בשבת שלא יכבה, שמחמת כפיית הכלי מונע האויר שסביב האור”. בחזיון הזה הסבה והמסובב גלויים, ואי אפשר היה להרב, שהיתה לו עין בוחנת ולב מבין, שלא יעמוד עליהם ויוציא מהם דבר להלכה. לא כן הדבר בענין מראות הצבעים, ששם דרושה לנו ידיעת סגולת האור וחוקי שבירתו בגופים השקופים ושיעוריהם בדקדוק, שמפני כך לא עמדו עליהם גם הפילוסופים הקדמונים, ולכן לא יפלא אם דברי הרב אינם מסכימים עם מציאות חכמת הטבע, כאשר נראה מיד.
ו) בספרו זה (סוף פרשת ויצא) יאמר: “בחינת לובן העליון, דהיינו בחינת אור עצמותו ומהותו של אין-סוף ב”ה, כמשל מראה וגוון לבן, שאינו דומה לכל המראות והגוונים, שהגוונים שלהם נתהוו על ידי צבע, מה שאין כן מראה וגוון לבן, היא עצמות הדבר ומהותו, ושלא נשתנה ולא נתהוה על ידי צבע". בספר “לקוטי תורה” (סדר אחרי), מפרש הרב דבריו יותר "כי בחינת הלובן אינו כשאר הגוונים, כי הוא בחינת עצמיות של הדבר ואין כאן דבר נוסף רק עצם הדבר לבד, מה שאין כן שאר הגוונים, שהם צבע שצובעים בו, אדום ירוק, שהצבע אדום הוא דבר נוסף על עצם הדבר, שהיה לבן, ועכשיו על ידי הצבע שנעשה אדום, ונמצא זהו הרכבה על עצם הדבר, מה שאין כן גוון לבן שהוא עצמי ואינו צבע 21. מדברי הרב נראה, שחשב את האור הלבן, לגוון טבעי ולעצם האור, ואת כל הצבעים האחרים לדברים בלתי טבעיים, ולכן היה אצלו האור הלבן אור פשוט, והגוונים האחרים – לאור מורכב שנעשה בידי אדם.
המושג הזה שעשה לו הרב על דבר מראות הצבעים, מראה בבירור כי זרים היו לו למודי חכמת הטבע בענין האור, גם לפי מצבם בזמנו. כל איש אשר ידיעת חכמת הטבע וקורותיה לא נעלמו ממנו ידע, כי בימים ההם כבר היה דבר מקובל ומוסכם אצל החוקרים, שהאור הלבן אינו אור פשוט, כי אם פתוך ומורכב. קרני האור היוצאים מן השמש, או מגוף אחר המאיר באור לבן, רבים ושונים הם מאד במינם, בשיעור שבירתם, במדת הגלים ובמספר הזעזועים שהם עושים ברגע אחד, אבל כל זמן שהם עוברים דרך אמצעי )מעדיום) אחד, או אפילו דרך אמצעים שונים, שהנם מוגבלים איש מאחיו על ידי שטחים מקבילים, הם מגיעים לעינינו זה בצד זה ומולידים בנו את מראה האור הלבן. לא כן הדבר בזמן שהם פוגשים באמצעי שקוף, שהשטחים המגבילים אותו הם נטויים זה לזה, כמו בזכוכית מלוטשת בתבנית משולש, או דרך טפות המטר שהן כדוריות בקירוב, אז קרני האור השונים אשר הלכו עד כה צמדים יחד, נשברים בעברם באמצעי הזה, נפרדים זה מזה ונבזקים, עד שהם נעשים כרצועה בעלת צבעים שונים, מפני שכל אחד מקרני האור נופל עתה בנקודה מיוחדת, וכל אחד מהם מוליד בנפשנו הרגשת צבע אחר, וכמו שאנו רואים זאת במראה הבזק (ספעקטרום) או במראה הקשת. צבעי הקשת והזכוכית המלוטשת יורונו, כי הגוונים השונים לא יולדו לנו על ידי מין אחד ממיני הצובעים (פאֶרבעטשטאפפע) כאשר יחשוב הרב, שהרי הזכוכית והמים נשארו זכים כשהיו, ובכל זאת נשתנו לגוונים הרבה, מפני שהאור הלבן נפרד בהם לחלקיו, שהוא מורכב מהם, ובאמת כאשר מצאה ידינו להפריד האור הלבן לחלקיו, כן נוכל לחזור ולהרכיב את הצבעים האלה ולהשיבם לאורם הלבן כבתחלה, אם נשוב ונקבץ את הגוונים השונים האלה )אשר בכלל נוכל להעמידם על שבעה) על ידי זכוכית גבנונית אל נקודה אחת, אשר תשוב ותופיע לעינינו באור לבן כבתחילה. וכן אם נעשה לנו לוח עגול ונחלקנו לשבעה חלקים בלתי שוים (כי אם לפי ערך מדת כל צבע וצבע במראה הקשת), על ידי משיכת שבעה חצאי אלכסונים ממרכז העיגול עד היקפו, ונצבע כל אחד ואחד מהחלקים באחד הצבעים מצבעי הקשת, ונסוב את העיגול הזה על מרכזו במהירות גדולה, אז יהפך העיגול לעינינו כלו לבן, מפני שכל הצבעים נבללו ונתלכדו יחד, ומולידים בנפשנו הרגשת מראה הלבן. על פי הדברים האלה נוכל לבאר לנו את כל מראות הגופים למיניהם: הגוף יראה לעינינו במראה לבן, אם אינו בולע אל תוכו כלל מקרני האור הנופלים עליו, אבל הוא מחזירם לאחור, עד שהם מזעזעים כלם את גלי האיתור, ומגיעים יחד אל העין ומולידים בה הרגשת האור הלבן. הגוף אשר יראה לעינינו שחור, בולע אל תוכו כל קרני האור ואינו מחזיר מהם כלל לעינינו. הגופים אשר יראו לעינינו צבועים בצבעים אחרים, כאדום, ירוק, צהוב, תכלת וכיוצא בהם, בולעים אל קרבם מקצת מקרני האור, והנשארים בהם, שהם מחזירים לאחור, משתתפים יחד להוליד בנו את הצבע שהגוף נראה בו לעינינו. האויר למשל הסובב אותנו בולע אל תוכו את קרני האור, שמדרגת שבירתם קטנה, כצבע האדום, הצהוב, הכרכום, ואינו מעביר ושולח אל עינינו כי אם את הגוונים אשר בסוף מראה הבזק, שמדרגת שבירתם גדולה יותר, ומתוך כך הוא נראה לנו כעין התכלת 22, והוא הדין לכל הגופים השונים למיניהם.
הדרך הזאת – לבאר את מראות הקשת וצבעי הזכוכית המלוטשת על ידי התפרדות האור הלבן לחלקיו בגשם השקוף, ואת צבעי הגופים על ידי כשרונם לבלוע מקצת קרני האור ולהחזיר מקצתם לאחור – ידועה היא לחכמי הטבע מימות החוקר האנגלי ניוטון, ((Neuton שהורה אותה בספרו הנדפס בשנת 1672, ועוד לפניו נתקרב אליה הפילוסוף הצרפתי דיקרט ((Descartes אשר מצא חוקי שבירת האור, ועמד על הדמיון שבין צבעי הקשת והזכוכית המלוטשת, ואשר היה הראשון שנתן פתרון נאמן להולדת הקשת בענן. דעת החכם ניוטון, אשר נתאשרה ונתקימה מכל החכמים הבאים אחריו, ויצאה מידי כל ספק על ידי נסיונות שונים וחזיונות אחרים של האור, היא ברורה ופשוטה על כך עד שאפשר להשתומם שלא עמדו עליה החכמים שהיו לפניו. אולם מלבד שכן הדבר בכל התגלות חדשה, וכספור הידוע מביצתו של קולומבוס, הנה באמת אי אפשר היה לעמוד על סבת מראה הקשת, כל זמן שלא נודעו חוקי שבירת האור (שנתגלו ע"י החכם סנעליוס, Snellius, בשנת 1621, וע"י החכם דיקרט בזמן ההוא), וכל זמן שלא יכלו לקצוב בדיוק את שיעור השבירה של כל אחד מצבעי הקשת. ובאמת היה מראה הקשת חידה נפלאה בעיני כל החכמים עד זמנם של דיקרט וניוטון. עוד בימים מקדם ראו החכמים שיש לקשת יחס וקשר עם מעמד השמש, והוציאו מזה משפט, שהקשת נולדת ברסיסי המטר אשר באויר, המחזירים לעינינו את נוגה השמש. אבל מדוע יראה לעינינו החזיון הזה רק בדמות חצי טבעת בזמן שרסיסי המטר ממלאים את כל האויר? השאלה הזאת נשארה תמיד בלי פתרון, עד שבאו חכמי הדורות האחרונים והוכיחו שאעפ"י שכל הטפות המרחפות באויר מפרידות את אור השמש לצבעיו, מכל מקום אין כחן שוה בשיעור האור שהן שולחות אל עינינו, כי רק הטפות העושות עם עין המביט זוית מן 1/2 400 עד 1/2 500. לערך, יש בהן די כח להוליד בנו הרגשת האור, מפני שהניצוצות היוצאים מהן מקבילים איש אל אחיו ומקובצים יחד כמו שבאו אל תוכן, מה שאין כן בטפות אחרות, שקרני אור השמש שבאו אל תוכן מקבילים, כשחוזרים לצאת מהם הם הולכים ומתפזרים, ולכן חלשים הם בכח אורם, ובטלים לגמרי לעמת כח האור היוצא מן הטפות שזויות נטייתן היא מן 1/2 400 עד 1/2 420. בדרך הזה נתבאר לנו גם אופן התהוות הקשת הכפולה, העושה עם עין הרואה זוית מן 500 עד 1/2 530 וההפוכה בסדר צבעיה, שגם היא אינה נבראת כי אם ע"י התפרדות אור השמש ברסיסי המטר, אלא שבקשת הפשוטה האור מושב לאחוריו מן השטח הפנימי שבטפה פעם אחת, ובקשת הכפולה הוא מושב ממנו פעמים, ולכן חלושה היא בכח אורה מן הפשוטה. גם מדת רוחב שתי הקשתות (הראשונה 20 והשניה 1/3 30 מסכימה בדקדוק עם החשבון הנוסד על יסוד שבירת האור. ההתרה הנכונה הזאת להתהוות הקשת נתנה לנו היכולת לברא לנו מושג נכון על דבר צבעי הגופים בכלל, דברים שלא היה בכח החכמים הקדמונים להסביר לעצמם בשום אופן. אריסטו, ראש חכמי יון 23 מבאר את צבעי הקשת על פי ההנחה שהאור הלבן נעכר בעברו דרך אמצעי שאינו זך ושקוף לגמרי. הדבר המאיר – יאמר – הנראה מתוך דבר כהה, יופיע לעינינו אדום; ככה יראה לנו עין האילן הירוק מתוך העשן, ועין השמש מתוך הערפל אדומים במראיהם. בדרך זה, כל אשר יחלש האור, או כח הראות, כן יתקרב צבע הדבר למראה שחור, בהתהפכו בראשונה לאדום אחרי כן לירוק (ככרתי) ובסוף למראה ארגמן כהה. אמנם האור חזק יותר בשפת הקשת החיצונה, מפני שהיא מרובה שם יותר בשיעור מסוים, באופן זה כאשר נעבור משפת הקשת החיצונה אל שפתה הפנימית, יצאו לנו בהדרגה מראה האדום, הירוק עד צבע הארגמן. בשיטה הזאת יחזיק עוד החכם De Dominis בתחילת המאה השבע עשרה, לפי דעתו האור כשהוא לעצמו הוא לבן, אך כאשר יתערב עם דבר שחור כל שהוא, יהפך לגוונים שונים; בראשונה לאדום, אחרי כן לירוק ובאחרונה למראה תכלת. בדרך הזה הוא אומר לבאר את מראה הקשת, באמרו, שקרני האור המגיעים אלינו מטפות המטר יש מהם העוברים חלקי טפה העבים יותר מאותם שיעברו חבריהם, ובאופן כזה יעלו לפנינו איש אחר אחיו כל צבעי הקשת. אבל נפלא הדבר, כי גם אחרי אשר נתפרסמה כבר דעת ניוטון הנכונה, נסה עוד המשורר האשכנזי Goethe להרוס את כל שיטתו, ולבנות על חרבותיה שיטה חדשה, שבעיקרה אינה אלא שיטת הקדמונים שחזר ויסדה. במאמרו “תורת הצבעים” (דיא פארבענלעהרע), יחליט המשורר, שהצבעים השונים נולדים בזמן שאנו מביטים על עצם מאיר דרך אמצעי עכור. עצם האור אין לו כל צבע, ורק בשעה שאנו מביטים עליו דרך אמצעי עכור, אז יופיע לעינינו במראה צהוב. אם עכירותו של האמצעי מתרבה, או כשהאמצעי נעשה עב יותר, אז יקבל האור בהדרגה מראה אדום צהוב, עד שבאחרונה הוא עובר למראה אבן האודם (רובין). מצד אחר אם נביט על עצם חשוך דרך אמצעי עכור, המואר על ידי האור הנופל עליו, אז יראה לנו במראה תכלת, והוא נעשה מזהיר יותר ויותר, ככל אשר תתרבה עכירות האמצעי; ולהפך נעשה חשוך ועב יותר ויותר, ככל אשר יהיה האמצעי שקוף יותר. בדברם כוללים וסבוכים כאלה, בדברים שיש בהם יותר מן הדמיון החזק של המשורר, ממה שיש בהם מן העיון המדוקדק של חכם וחוקר, יסד גֶטֶה את שיטתו המסוכסכת על דבר שבירת קרני האור ומראות הצבעים, הפוטרת עצמה מכל חשבון, ומשתמטת מתחת יד כל נסיון ובקורת. חכמי הטבע עוברים על כל השיטה הזאת בשתיקה, ולא יביאוה כלל בספריהם. ואך כותבי קורות המדעים לבד יזכירוה בדרך הלוכם, כעין השערה נפלאה ומוזרה. דברי הפילוסופים שהבאנו, וביותר דברי גֶטֶה שכבר היה לפניו השיטה הנכונה של ניוטון, ובכל זאת רצה לעשות לו דרך חדשה, המסכמת בסקירה הראשונה יותר עם מראה העין והעיון הגס מספיקים לנו ללמד זכות על הרב, שלא ראה את דברי ניוטון, והוצרך לברוא לעצמו את מושגיו בדבר הצבעים, ולא יפלא עוד בעינינו אם אינם מסכימים עם תוצאות חקירות חכמי הטבע ונסיונותיהם. אלו ירד הרב לחקירות האלה, כמה היה יכול להסתייע בהן לענין שיטתו במהות העולם והמציאות, ולברר על ידי זה את הרעיון העמוק החביב עליו כל כך והעובר דרך מחקריו באלהות, שעצם הדבר לעצמו (דאס דינג אן זיך) איננו כלל כפי מה שהיא מתגלה אלינו, שהרי כל מה שאנו רואים, אינו אלא תולדות זעזועי האיתור הדק מן הדק, והמתנועע בתנועה גולשת (וועללענארטיגע בעוועגונג) לרגלי סבה המעוררת אותו, אבל אין לו כל צבע מיוחד לעצמו. ואם נצעד עוד צעד אחד – כאשר בלי ספק היה הרב עושה כן – לא יקשה עוד בעינינו להאמין, שהדבר המתגלה לנו בתמונת גוף ממשי וחומר גשמי, באמת איננו במציאות כלל, ואינו אלא טעות החוש, וכי רק עצם אחד רוחני הוא ממלא כל עלמין, המתגלה לנו תמיד בתמונות שונות, לפי כשרון כח השגתנו, וכדרך שיאמינו הפילוסופים בעלי שיטת הרוחניות, שהרי סוף כל סוף גם בעלי שיטת הגשמיות זקוקים לומר, שכל החזיונות המתגלים לנו אינם אלא תולדות תנועת “העצמים הפרדיים” או “הפרודות” (אטאמען), שאינם נתפשים בחוש, ותולדות זעזועי הזהריר או האיתור שאינו יוצא גם הוא מכלל השערה 24.
ז) בסידור (שער הל"ג בעומר) יאמר הרב: “דהנה נלאו כל חכמי הטבע להבין ולהשכיל סבת החמימות בקיץ והקרירות בחורף, משום דעל פי חכמי התכונה אין מרחק השמש לצד מן הצדדים או לגובה, לא מעלה ולא מוריד כלל, כי לפי ערך קטנות כדור הארץ לגבי כדור השמים, שהוא כערך גרגיר חרדל בתוך היקף והיכל גדול, מה יועיל חום השמש בנטיתה לצד מן הצדדים בעיגול כדור השמים לענין חימום, לחמם אויר הארץ בקיץ, או למעט החום בחורף, כשהולכת בשפולי כדור השמים?”. מפני הקושי הזה: “שהארץ הוא כגרגיל חרדל”, יחשוב הרב לדבר נמנע, שהשנויים באויר הארץ יהיו תלויים בפעולות גופים גשמיים, והוא מייחס אותם לפעולות כחות רוחניים השולטים בעולמות העליונים, ופועלים פעולתם בעולם השפל, כחות שאינם נופלים תחת חוקות הטבע, ויש בהם מקום לכח הדמיון ליחס להם סגולות כרצונו. והרב מחליט ואומר: “אלא שהענין מורה חדוש ההשפעה מאין ליש למעלה מדרכי הטבע וכו'”, “שהשמים ישפיעו גם הקור והחום בקיץ ובחורף וכו', ועל כן יתחלקו המקומות בארץ בשינוי אופני הקור והחום לפי אופן מקום מעמדם נגד שרשם בשמים המשפיעים לנוכח ראשם”, וקושיתו מתישבת לו עתה מאליה: “שאף על פי שהארץ כגרגיר חרדל”, הנה אין הכח הרוחני צריך להשתוות כלל “בבחינת המקום”, עם אותו שהוא משפיע עליו, ואין הכרח “שהחלק המושפע ממנו בארץ יהיה לפי ערך מקום לגבי שטח מקום שבכדור השמים” “אך שיהא המקבל מכוון כנגדו” “וממילא נמשך הקרירות [והחום] לנוכח ראשי אנשי אותה המדינה, שמכוונים נגד לנוכח אותו השטח הגדול אשר בשמים” 25, כי בהשפעה רוחנית שטח המקום לא מעלה ולא מוריד, אחרי שאין כח הרוחני מגדר וסוג שטח מקום, כדמיון המחשבה שתוספת (צ"ל: שתופסת) שטח גדול בסקירה אחת". לא יפלא כלל בעינינו דרך הרב אשר ישתדל תמיד לבטל את מציאות החומר בפני הכח הרוחני, אם גם הפעם בחר לו סבות רוחניות במקום פעולות גשמיות, אבל יש לתמוה עליו, איך שם תהָלה בכל החוקרים, ופסק ואמר כי “נלאו כל חכמי הטבע” להבין הסבה, בעת אשר אין בדבר כל קושי כלל, ובעת שקושיתו מזה שהארץ היא כ"גרגיר חרדל" אין לה כל יסוד ושורש 26?. את המאמר הזה לקח הרב מספרי חכמת התכונה 27 ודמה להקיש ממנו על התחלקות החום על פני כדור הארץ, ודן דינו על פיו, כי מפני קוטן כדור הארץ צריך החום להתפשט על פני כלו בשוה ובבת אחת, מבלי הבדל במדת מדתם מקור החום מן הארץ או בנטייתו לצפון או לדרום, אחרי שבין כך ובין כך הוא רחוק ממנו הרבה, אבל הרב היה יכול להקשות קושיא גדולה הרבה יותר, שהרי באמת השמש בתקופת תמוז רחוקה מן הארץ יותר ממה שהיא רחוקה בתקופת טבת, ומדת מרחקה בשני הזמנים האלה הוא בערך 31 אל 29, ואם כן ראוי היה שיהיה החום בתקופת טבת גדול מתקופת תמוז (ומפני שהחום מתמעט בערך הפוך למרובע המרחק, ראוי היה שתהיה מדת החום בטבת גדולה ממה שהיא בתמוז כערך 8 אל 7). אבל באמת אין הנידון דומה לראיה, קוטן הארץ וריחוקה מן השמש גורמים רק זאת, שהאיש העומד על פני הארץ והעין הנתונה כביכול במרכזה, רואים את השמש כמעט במקום אחד ברקיע (כי זוית חלוף המראה אינה עולה כי אם 95, "8), אבל שנויי הקור והחום בארץ, מקורם עוד בסבות אחרות. שיעור השפעת החום תלוי במרחק השמש מן הארץ (ולכן חום הקיץ בחצי הדור הדרומי, שזמנו נופל בזמן שהשמש בתכלית קרבתה אל הארץ, גדול מחום הקיץ בחצי הכדור הצפוני, שזמנו נופל בתכלית רחוקה מן הארץ), אבל שיעור קבלת החום, מלבד הכשרון המיוחד אשר למקבל, תלוי בתנאי ראשו, בשיעור הזוית שניצוצי השמש עושים עם שטח האופק, שכל מה שהם מרבים לנפול בשפוע, פעולתם חלושה יותר. וכמו שאנו רואים זאת בשינוי חום האויר במשך היום, שמרחק השמש ונטיתה אינם משתנים, כי בבקר בשעה שניצוצי השמש עושים עם האופק זוית קטנה, גם מדת החום קטנה, והולכת ומתגברת עד חצות היום, שהזוית הזאת היא בתכלית גדלה, ומשם והלאה החום פוחת והולך יחד עם מדת הזוית, וכן חוק ידוע הוא בחכמת הטבע, מאושר ומקוים על ידי הנסיון והעיון גם יחד, ששיעור החום או האור, אשר יקבל הגוף מן המקור המשפיע אותם עליו, בין שהוא רחוק בין שהוא קרוב, הוא כערך בקע הזוית שנצוציו עושים עם שטח הגוף המוחם או המואר. אם יפלו עליו נצבים, אז יקבל הגוף את כל השיעור המושפע עליו, ואם דרך משל יעשו עם שטחו זוית בת 300 אז לא יקבל כי אם מחציתו, אם נקח גוף מעוקב, ונעמידהו נגד השמש, באופן שנצוציו יפלו נצבים על אחת הדפנות, אז תקבל הדופן ההיא את כל החום והאור, בזמן שיתר הדפנות לא יקבלו מהם כלום, אבל אם נעמידהו באחת מפינותיו נכח השמש, באופן שנצוציו יפלו מקבלים אל אלכסון המעוקב, אז יקבלו שלש דפנות את החום ואת האור בשוה, אבל שיעור החום שתקבל כל דופן לא יהיה כי אם נ"ז אחוזים למאה (כי בקע זוית הנטיה יהיה אז V1/3 ממה שקבל הגוף באופן הראשון. מן הדברים האלה אנו למדים, כי סבת החום והקור תלויה רק בנטיית השמש לצפון או לדרום, לא מפני התקרבותה אלינו או התרחקה ממנו ברחבי שמים, כי אם מפני ששיעור הזוית שניצוצי השמש עושים עם האופק מתרבה או מתמעט. ברוחב ° 53.5 לדוגמא נמצא שנצוצי השמש עושים עם האופק בתקופת טבת אך 300 ובתקופת תמוז 770, ונמצא ששיעור החום אשר יקבל המקום הזה במקרה הראשון אינו כי אם בערך מחצית ממה שיקבל במקרה השני, ואם נוסיף להתבונן ששיעור הזמן שהשמש נמצאת על האופק בתקופת טבת, הוא רק מחצית הזמן שהיא משמשת ביום תקופת תמוז, נמצא ששיעור החום שיקבל המקום בטבת אינו אלא כרביע ממה שיקבל בתמוז (מובן מאליו שכל המספרים אינם כי אם בקירוב).
אמנם לא הקיץ והחורף בלבד – אשר אותם הרים הרב על נס, ואשר כל עין רואה כי שומרים הם את מועדיהם. פחות או יותר, ובפרט כל אשר נקרב אל אזור החם – תלויים בשמש, במהלכה ונטייתה על שטח האופק, אבל גם מראות הטבע האחרות וחליפותיהן על הארץ, אשר למראה עין אין להם כל סדר ומשטר, כירידת הגשם ונפילת הברד, עליית החום וירידתו פתאם, התרבות כובד האויר והתמעטותו בלי סבה נראית, נשיבת הרוחות המשתנה תמיד, היובש והלחות היוצאים חליפות, וכל המון החזיונות אשר באויר, כלם אין להם מקור אחר זולתי בשמש, המשפיעה את כחה על הארץ, ועל יתר כוכבי הלכת מבני לויתה, ואין לכל כח אחר בשמים חלק בהם. אך מפני שפעולות השמש על הארץ שונות מאד, לפי מצב המקום בין עגול המשוה והציר, לפי גבהו מעל לשטח הים, לפי ערך הרריו ועמקיו ותבניתם, לפי קרבתו אל הים, לפי נהרותיו ויערותיו, לפי תכונת המקום וקרקע האדמה, ולפי כשרונם לקבל את השפעת השמש, – בגלל כל הדברים האלה ורבים אחרים כיוצא בהם, סבות כל החזיונות האלה ותנאיהם נעשים סבוכים ומסובכים ביותר, עד אשר אין לאל ידינו עוד להגיד מראש את עת בואם בכל נקודה ונקודה מכדור הארץ. אולם חוקרי הטבע עם קשה-עורף המה, לבם לא יפול עליהם ולא ישובו מפני כל מעצור, ברוח נכון ובטוח לא יחדלו לצעוד קדימה ולכבוש לעצמם נתיבות חדשות למען הגיע אל מטרתם. יודעים המה, כי לפנים היה כן גם גורל חכמת התכונה, כי האדם בימי קדם לא יכול למצא ידיו ורגליו בחזיונות השמים, ולעשות לנפשו אפילו ציור כל שהוא מבנין העולם ומסדור המאורות והככבים ומהלכם, והיה זקוק לתלות הכל בכחות שהם למעלה מן הטבע, ולפתור לו את כל החזיונות על פי דמיונות האסטרולוגיה; ועתה אחרי יגיעת אלפי דור, הנה יש לאל ידינו להגיד מראש כל חזיון וכל מראה ברקיע שמים ולקצוב זמנם כחוט השערה. כדבר הזה יקרה לאחרונה את ידיעות המטרולוגיה. עמל החוקרים לא יעלה בתהו, סוף סוף הצעיף אשר תתעלף בו הידיעה הזאת יוסר, ועוד יבא יום ועלתה גם היא על המדרגה הגבוהה, אשר עליה עמדה זה כבר אחותה חכמת התכונה. וכשם שיש בידינו כהיום לחשוב בדיוק את הרגע אשר בו תקרה קדרות לשמש או לירח במקום פלוני ופלוני, כן נוכל בימים הבאים להגיד מראש את רגע ביאת המטר ונפילת הברד וכיוצא בהם בכל מקום ומקום בארץ. הכנסת כחות נעלמים בחקירת הטבע, כחות שאין ביד האדם להתחקות עליהם ולדקדק עמהם כל עיקר לא הועילה מאומה להתפתחות המדעים ולהכרת האמת בנפלאות הבריאה. אך מאז החלו חכמי לב וכבירי רוח להסיר מעל דרכם את השטן הזה, ולהושיב במקום הדמיון המתעתע את הנסיון המדויק, את חכמת השיעור ואת ההגיון הישר, מן העת ההיא כביר מצאה ידם להבין ולהשכיל יותר ויותר במעשה אלהים כי נורא וכי נשגב הוא.
ח) בסדר תפלה שלו (בפירוש לפסוק “זכר רב טובך”) מבאר הרב את ההבדל שבין רבוא פעמים אחד ובין רבוא אחת, שבאופן הראשון אנו סופרים את כל האחדים בפועל ומונים אותם אחד אחד, ובשני אנו מספרים ומודיעים לאחרים את המספר המנוי, שעלה כבר בידינו, אבל אין אנו סופרים אותו עתה; באופן הראשון יש בידינו רבוי האחדים, ובשני אנו מתבוננים על הרבוי הזה כאלו הוא אחד; באופן הראשון יש לנו עסק עם מדת האחדות האמתית, ובשני בראנו לנו מושג חדש שקראנו את שמו בשם רבוא. או לפי סגנון לשונו של הרב: באופן הראשון המספר הוא “בחינת מספר עצמי ואמיתי”, ובשני הוא רק כמו קריאת שם בלבד לזכרון דבר", “כמו שיעשה אדם סימן לזכרון על איזה ענין, אין באותו סימן הלבשה והוראה מאותו ענין כלל, וכמו קריאת שם לאדם, שהוא רק להכיר ולזכור על ידו זאת גופו ומהותו”, “שאין מהות האדם בשם זה, רק השם הוא לסימן ולזכרון בלבד”. במספר רבוא ובמספרים אחרים כיוצא בו, רואה הרב רק את “הקטנת גדלות המספר, שהמספר הגדול הכולל בתוכו עשרת אלפים אחדים, מנויים אחד אחד, נתפס עתה בשכלנו בדבור אחד כאחדות אחת, ועל הדרך הזה נוכל ללכת הלאה להתבונן על מספר רבוא רבבות ולקרא לו שם חדש, כאלו הוא אחדות אחת וכו' וכו'”. זו היא תמצית דברי הרב הארוכים וכוונתו שם, אף שאין זה לשונו 28. ואף על פי שלכאורה אין אנו מוצאים פה כל חדוש בחכמת החשבון, ואנו רואים פה יותר אך את נטיית הרב להתבוננות ההגיונית וגדירת המושגים הכלולים בשמות, בכל זאת מצאתי לנכון להביא פה את דבריו, מפני שאנו מוצאים בהם את המושג של “אין- סוף” במספרים, אשר נולד בזמן אחד במוחם של ניוטון ולייבניץ (Leibnitz), (והם המספרים הידועים היום בשם “גדולים בלי תכלית” ו"קטנים בלי תכלית") שכבר הרגישו בו גם חכמי יון הקדמונים, אבל לא דקדקו לגדור את מושגם היטב כאשר עשו האחרונים, ואני רואה בדברי הרב דמיון גדול עם דברי האדם הגדול בענקים ארכימדיס ((Archimedes, אשר כבר עשה לו מושג נכון בשעורים הקטנים לבלי תכלית, ומצא על פיהם את מדת השטח המוגבל על ידי קו העקום הידוע בשם “פַרַבֶּל”. החכם הזה אשר חי במאה השלישית לפני המספר הרגיל, יאמר בספרו “מספר החול” (המובא גם בספר “גבורת ה'” ליש"ר מקנדיאה, מדרגה ל"ד): "רבים חושבים, גֵלון (Gelon) מלכי, כי מספר החול גדול לבלי תכלית.., ויש עוד אחרים, אשר לא יחשבו את המספר הזה לבן בלי גבול, אבל יאמרו, כי לא קרא עוד איש שֵׁם למספר גדול, אשר ירבה ממנו 29,
(בהערת שוליים 29 צריכה להופיעה תבנית שצויינה באות A. בשל קשיים טכניים בהצבתה בהערה, התבנית מופיעה במקום זה - הערת פרויקט בן יהודה)
4
4
4
4
אבל אנכי אשתדל להוכיח במופתים הנדסיים, אשר לא תכחיש אותם, כי בתוך המספרים שקראתי בשם בספרי הנמצא ביד צעאוקסיפיוס ((Zeuxippos, יש כאלה אשר לא לבד שיגדלו ממספר ערמת חול שגדלה שוה לכדור הארץ… אבל [יגדלו] מזו שתעבור בגדלה גודל עולם ומלואו". לתכלית זו יברא לו המהנדס היוני לאחדות את המספר רבוא רבבות אשר נכנהו בשם “שמינית” (octade, מפני שהיא המדרגה השמינית מן המספר 10) וכמו שבחשבון הנהוג, אנו מעלים את המספר עשרה למדרגות שונות, שמאה היא המדרגה השניה ממנו, ואלף הוא המדרגה השלישית וכו', ככה יעשה ארכימדס עם המספר שבחר לו, עד שהשמינית שעלתה למדרגת רבוא רבבות, או שהוכפלה על ידי עצמה רבוא רבבות פעמים (בדרך המספר שלנו נכתב על ידי 1 עם 800 מיליונים אפסים) תקרא אצלו בשם תקופה (פעריאדע), באופן שהתקופה השניה אצלו צריכה לְהִכָּתֵב לפי דרכו על ידי 1 עם 80000 ביליונים אפסים, אם נחשוב את הביליון למיליון פעמים מיליון בסדר ספירת האשכנזים (עיין Mathematische Beiträge zum Kulturleben der Völker von D-r Moritz Cantor צד 149). כל המספרים המפליאים האלה, אשר גם הגדול בבעלי הדמיון לא יוכל לעשות לעצמו גם מושג קל מהם אין בהם כל תועלת מעשית, אבל בכל זאת הם מרחיבים דעתו והשגתו של אדם, והם מולידים בלבנו את הרעיון שיש בכחו לישא וליתן גם בשיעורים בעלי בלי גבול וקץ, ולחשוב את מה שאינו כאלו ישנו, להתבונן על המושגים האלה על צרופיהם וצרופי צרופיהם, ולהתחקות על תולדותיהם ותולדות תולדותיהם כאלו הם נמצאים באמת. הרעיון הזה נתאשר עוד יותר בדורות האחרונים, כשנגלו לנו המספרים המדומים (איממאגינערא=צאהלען) השונים למיניהם, שאינם נמצאים ואינם יכולים לְהִמָצֵא במציאות, ובכל זאת כאשר נבצע עליהם מעשה החשבון יובילו אותנו לתוצאות נאמנות. כל הדברים האלה הביאו את הפילוסופים שבין חכמי ההנדסה לתת לנפשם מושג אחר על ענין השיעור ההנדסי (מאטהעמאטישע גראֶסע), עד שנפלו כל הגדרים שנתנו לפנים למושג הזה. וכפי שהוכיחו חקירות גראססמאנן, האַנקעל, דעדיקינד, העלמהאלץ קאנטאר וחבריהם. הנושא שתתעסק בו חכמת השיעורים אין זקוק כלל להלקח מן המציאות, וכי נוכל לברא לנו מושגים ככל העולה על רוחנו, ובלבד שיהיו גדורים בדיוק כראוי, ואם במשך החשבון לא נחטא לגדרים שנתנו להם מראש, יולידו לנו תולדות נאמנות, ופעמים רבות יביאו לנו תועלת גם במעשה.
בקצרה, כח החושב אשר לאדם הוא נושא בפני עצמו, ואינו זקוק כלל אל המציאות אשר מחוצה לו, וכחלק אלוה ממעל יש בו ממדת קונו כביכול, לברא על ידי צרופי אותיות וקשור המושגים ההגיוניים יצירים רוחניים כרצונו בלי קץ ובלי תכלית; יצירי אמת, שפעולתם אמת וחותמם אמת.
הרב לא היה יכול לדעת מכל הצפונות היקרות האלה, אבל רוחו הרגיש שיש במושג המספרים הגדולים ענין נשגב ונעלה, וכפי דרכו נגע בו נגיעה קלה בקצה קולמוסו.
ט) דברי תורה וחכמה קשורים זה בזה וחרוזים זה בזה, וכן גם אנו שהצבנו לנו למטרה להתחקות רק על החכמות הלמודיות או המדוקדקות, שנמצאו בדברי הרב, לא יכולנו לשמור את הגבול לדקדק בו כחוט השערה, ולאחרונה בסימן הקודם, נגענו באצבע קלה גם בפילוסופיה של ההנדסה. סוף סוף כל התחומים נוגעים זה בזה ויונקים זה מזה, ואי אפשר להפריד ביניהם. כל הפילוסופים אשר מעולם, מפיתוגרס אפלטון עד דקרט ליבניץ וקנט בעמים, ומרס"ג הראב"ע הרמב"ם עד הרלב"ג קרשקש ושפינוזא בישראל, כלם היו גדולים בחכמות הלמודיות, כל אחד מהם כפי מצבן בזמנו, כי כל החכמות כולן נובעות ממקור אחד: מבקשת האמת המוחלטת ומן ההתבוננות העמוקה החוקרת לכל תכלית. הרב לא היה לא פילוסוף ולא מהנדס מעמיק רק בלמודיות, כי חנוכו ותעודת חייו סללו לו מסלה אחרת בעולמו, אבל שתי המדות שאמרנו, בקשת האמת והנטיה להתבוננות, העושות את בני העליה להוגי דעות וחושבי מחשבות, נמצאו בו במדה גדולה מאד. ובכל אשר ראינוהו והכרנוהו לאיש מעשה, יודע דרכי החיים ועוסק בצרכי הצבור, הנה ביותר היה נוטה מטבעו להשקיע כל רוחו רק בעיון העמוק ובהתבוננות המופשטת, ולולא היה זקוק להטפל גם בחיי מעשה, בלי ספק בחר לו להתבודד רק בארבע אמות של מחשבה, שהיתה חביבה לו מכל, וכדרך שאמרו (ירושלמי פאה פ"א): אפילו כל העולם כולו, ואפילו כל מצותיה של תורה, אינן שוות לדבר אחד מן התורה. הרעיון הזה בוקע ועולה מדברי הרב, שכתב בעצם ידו ברגעי חייו האחרונים, אשר הובאו בפנים הספר בחלק ראשון (עמ' 164) ולא נתפרשו במקומם.
הרב בעמדו על הגבול המפריד בין העולם העובר – עולם השקר – ובין העולם הקיים – עולם האמת, ובהתעתדו להדָבק במקור החיים, באל עולם, מפנה את כל מחשבותיו לדעת ולמצא את תכלית בריאת האדם ומטרתו בארץ, ומה היא הדרך הישרה שיבור לו בחיים. והרב מתבונן על דברי העולם הזה, אשר לפי דברי האגדה (ב"ר פ"ח) עוד לפני בריאתו היו חסד ואמת מדיינים בו, הסד אמר יברא, ואמת אמר אל יברא, השליך הקב"ה אמת ארצה, ועולם, כדברי הרב, “בחסד שאינו של אמת נבנה”. והרב מוצא, כי אין טוב לאיש הרוח, בלתי אם להתרחק בכל כחו מעניני העולם הזה, המעבירים את האדם על דעתו ומטים אותו בעל כרחו ממטרתו הנעלה והנשגבה. והמטרה הזאת היא רדיפת האמת המופשטת וההתבוננות במושכלות הכלולות אצלו במלת תורה, וששתיהן אחת הן אצל הרב, כי אין “אמת אלא בתורה”. הנפש הנעלה והגבוהה בשרשה במדרגת האמת, תורתה רוחנית ועבודתה רוחנית, אבל “הנפש השפלה באמת לאמתו בשרשה, עבודתה היא תורה גשמית בין לה בין לאחרים (בין אותה שהיא מלמדת לעצמה בין אותה שהיא מלמדת לאחרים) וגמילות חסדים גשמית” ואינה נקיה מפניות. האמת היא המתנה היקרה האחת, שהיתה לו להקב"ה בבית גנזיו, ושחלק אותה באהבתו לבחיר היצורים, לאדם הנברא בצלמו. האמת היא המדה האחת הראויה שישתמש בה העולם, לא רק בעיון והתבוננות מופשטת בלבד, כי גם בדברים שבמעשה: בחיי היחיד והצבור, וכל נטיה כל שהיא מדרך האמת ואפילו הטיה כלפי החסד, אינה רצויה בעיני המקום. חכמי ישראל הקדמונים, שנוכל לכנותם בסגנון התלמוד בשם: “תקיפי קדמאי”, שהיו תלוים רק בדעת עצמם, היו מתנהגים לדעת הרב, רק בדרך האמת, ועושים כל מעשיהם רק על פי תורת אמת, ואפילו הדברים שאנו קוראים להם עתה בשם מעשה צדקה וחסד, היו נחתכים רק בתוקף כח האמת ומדת משפט המוחלטת, וגדולי הדור הַמְעַשִׂים את העם לא היו זקוקים להתרפס ולשאת פנים לעושים, אשר בנוהג שבעולם אין האמת נר לרגלם. “בדורות הראשונים, שרוב העבודה היתה בתורה, היה רוב החסד נכלל באמת, דהיינו גדול המעשה, דכופין וממשכנין על הצדקה על פי תוקף תורת אמת”. כי לדעת הרב עשיית הטוב והחסד אינו דבר של רשות, התלוי רק ברגש לבו ורצונו של כל יחיד ויחיד, אשר חליפות רבות לרוחו, אך חובה ומצוה המיוסדת על תורת אמת, שיסודותיה קיימים ונאמנים לעולם ועד. אבל בצוק העתים האלה “בעקבתא דמשיחא”, שנדלדל כח התורה, ותופשיה נפלו מאיגרא רמא לבירא עמיקתא – ממרום עולם האצילות אל תהום עולם המעשה, “שנפלה סוכת דוד עד עפר בבחינת עשייה”, וחכמי הדור אינם תלויים עוד בדעת עצמם בלבד, ובעל כרחם הגדולים נזקקים לקטנים, וצריכים לבטל דעתם מפני דעת אלו שהיכולת בידם, אין עוד בהם די כח לתת להאמת את השלטון היחידי הראוי לו בעולם, “העבודה העיקרית שלהם היא בבחינת עקביים, בלי תורת אמת”,שהיא יסוד העולם כלו, גופין ויערכין דיליה". בתנאים כאלו קשה גם לבעל רוח כביר להחזיק מעמד, ומי שנשמתו איננה גבוהה מעל גבוהה במדרגת האמת לאמתה, אי אפשר לו שלא יוַתר לפעמים על האמת בדברי עולם הזה “שכולו שקרים וחסדים” (מה נמרצו דברי הרב, שהחסד והשקר הם בעיניו רק שמות נרדפים!) וזקוק הוא פעמים הרבה להסביר פנים להשקפת בני אדם הרחוקים ממנו, בהשקפותיהם “על ידי קירוב הדעת [ובקשת] עצות מרחוק בעניני וצרכי בני ביתו”, דברים אשר “רובם ככולם הם דברי שקר”, “אבל אי אפשר שיעשו בענין אחר”. ולכן גם החסד והצדקה שעושים עתה גדולי הדור, הַמְעַשִׂים אחרים לעבודת הצדקה, אינו חסד של אמת “ורוב החסד ככולו הוא שלא על פי תורת אמת גם בגדול הַמְעַשֶׂה” ונמצא שאין עבודתם שלמה, כי אף על פי שכונתם טובה ורצויה, ותכליתה עשיית חסד של אמת לאמתה, מכל מקום הדרכים שזקוקים להשתמש בהן “והתקרבותם לדעת העושה ורצונו הטוב”, אינם מכוונים עם האמת, ואחר אשר “סוף מעשה במחשבה תחילה ונעוץ תחלתו בסופו”, נמצאה המחשבה שהיתה טהורה ונעלה בתחלה, נפגמת בסופה על ידי המעשים ההולכים עמה צמדים, וסוף סוף אינה יוצאת, מכלל עברה לשמה. והרב באהבתו הגדולה והיתירה לאמת חותמו של הקב"ה, מוסיף להעביר תחת שבטו גם את המדות המשובחות שמקורן ברגש הלב, ומוצא שגם הן אינן נקיות מדופי. אין לך מדה טובה מזו שטבועה בכל נפש עדינה לנוד לקשה-יום ומוכה אלהים, לדבר על לבו דברים נחומים, לחזקו ולאמצו ביראת ה', כי ישוב אל אלהים וירחמהו, אבל בעיני הרב לא זַכָּה גם היא לגמרי, מפני שאינה מכוונת תמיד אל האמת, ראשית חובתו של אדם. “וגם אין כן דרך האמת, והיא שפלה, אז (בבוא איש נענה לשאול בעצת גדול הדור) לנחמו, לקבל באהבה, או לעזרו לפשפש במעשיו, וישיב אל ה' בצר לו וירוח לו רֶוָח”. הדרך היחידה המתאמת עם רוח הרב, שאינו מביע אותה בשפה ברורה, אבל מבצבצת היא ועולה ממקומות רבים מספריו, הדרך שראוי לאדם הנעלה לאחוז בה – אף שהיא קשה ביותר ונמנעת לגמרי, אם אין לאיש אשר דבר לו אליו כל צד משותף בדעות – איננה להוריד את עצמו אל מדרגת האדם הנופל ממנו במעלות הנפש, ולהתקרב לדעתו והשגתו הרחוקות מן האמת, כי אם להפך להרימו ולהגביהו אליו ולהעמידו אתו יחד על אותה המדרגה הנשגבה, ששם ישורו האמת והבינה ממשלה שאינה מוגבלת. ואין עוד מלבדן, למדרגה ששם אין מקום לפגעי הזמן ולמקרי העולם השפל. האמת היא אצל הרב המטרה היחידה אשר על האדם לשאוף אליה כל ימיו מבלי נטות ממנה כחוט השערה, והבינה היא אצלו אֵם ליראת ה' ולאהבתו, והאמונה המיוסדת עליהן, היא אמונת היחוד, נותנת לאדם מנוחה שלמה ושמחת הנפש (והוא מכניס את הכונה הזאת במקרא “אם הבנים שמחה”), ועל האמונה הצרופה הזאת הוא מעמיד כל התורה והמצות, ומוצא לדבריו יסוד בדברי חבקוק לפי דרשת התלמוד (מכות כ"ד): וצדיק באמונתו יחיה, “יחיה דייקא”, חיים של תענוג הנפש, חיים שאינם פוסקים לעולם “תחיית המתים ממש” במקור החיים הנצחיים (עיין תניא פרק ל"ג).
-————-
חתימה. 🔗
בחפצי לעשות את מאמרי רצוי לרוב הקוראים, השתדלתי לתת לו פנים מסבירות, ונשמרתי מאד מהכניס בו תמונות הנדסיות, שלא להבעית בהן את הקורא הבינוני, אבל כדי שלא יאמר עלי המבקר שאני אומר דברים בלי טעם, משיג ומחליט בלי ראיה, הנני להשלים פה את החסרון, ולהביא בזה את התמונות הנצרכות לחשבונות שיעורי הנשף ובין השמשות, כדי שיוכל הקורא המעמיק יותר לבחון דברי ולדקדק בהם כראוי.
אם בצורה (I) שלפנינו יורה העגול H Z P T N על אופן הצהרים במקום ידוע בכדור הארץ, H S T על אופן המקום ההוא, Z על נקודת קדקדו, P על ציר הארץ הצפוני, S מקום מרכז השמש לעת שקיעתה, S' מקומה בסוף זמן בין השמשות, ונסמן את
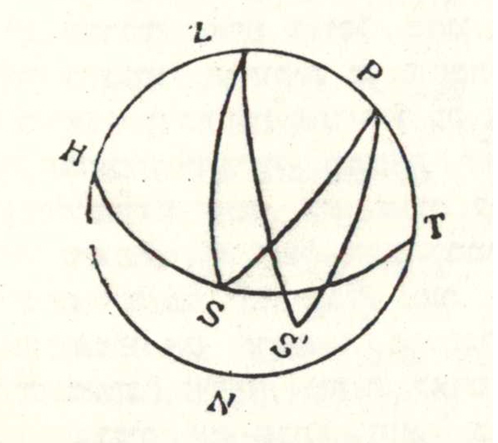
רחב המקום הנתון באות φ, נטיית השמש מקו המשוה באות δ, ומרחק השמש מנקודת
הקדקד בזמן סוף בין השמשות 30), והוא הקשת Z S', על ידי 900 + c,
הנה במשולשים הכדוריים P S' Z, P S Z, שצלעותיהם ידועות לנו,
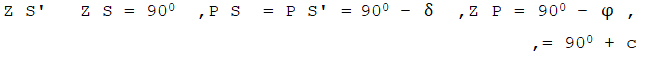
נמצא את שתי הזויות S P Z, S' P Z המודדות את השעות לעת השקיעה וזמן סוף בין השמשות, שנכנה את הראשונה T ואת השניה t+ T, נתונות לנו על ידי שתי המשויות האלה:
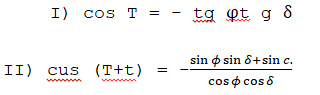
על ידי חלוף קוי המשולשים, אחרי שנגרע את שתי כתפות המשוה האחרונה מן המספר I, נוכל לתת לה תמונה כזאת, המוכשרת יותר לחשבון על פי לוחות המגבילים:
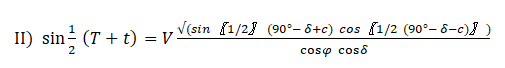
שלוש התמונות האלה הובאו כבר במאמרי “בין השמשות” (האסיף תרמ"ח צד 270); אבל פה פגשנו במרוצת דברינו עוד בשאלה אחרת: למצוא שיעור בין השמשות הקצר וזמנו. השאלה הזאת נפתרת בדרך כזה: אם בצורה הקודמת נדמה ברעיונינו, שהמשולש S P Z ישנה את מקומו ויסוב על הציר P, עד שצלעו P S תתאחד עם הצלע Z S', והנקודה S שהיא מקום השמש בסוף בין השמשות (שנציינה מעתה על ידי האות S בצירוף אחד הסימניות 2, 1, 0) תתלכד עם נקודת S' (כי מדה אחת לשתי הקשתות האלה, שכל אחת מהן היא תשלום נטיית השמש), והצלע P Z, שהיתה בתחלה באופק הצהרים, תרד בתנועתה למטה,
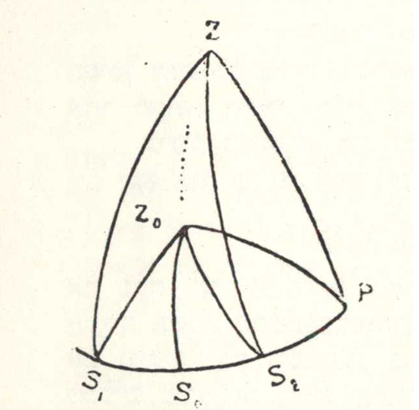
ותקבל מצב חדש P Z0, הנה מובן מעצמו, שהקשת המחברת את נקודת הקדקד P עם מרכז השמש בסוף בין השמשות, זקוקה לקבל אחד משלשת המצבים האלה: או שתעבור דרך נקודת Z0, ותפגע בנקודת S0, או שתפול לשמאלה ותפגע בנקודת SI, או לימינה ותגיע לנקרודת S2, כמו שנראה לפנינו בצורה (2). מדת הזוית Z P Z0 הנולדת על ידי סבוב המשולש S P Z על הציר P, המודדת את זמן בין השמשות, אשר נציינה באות t, הסגורה בין שתי צלעות שמדתן קבובעה וקיימת (שוה לתשלום גובה הציר) תלויה רק במדת הצלע Z Z0 שכנגדה, ונקל לראות שהקשת הזאת ועמה מדת זמן בין השמשות, תהיה בתכלית קטנה, בזמן שהקשת S0 Z תעבור דרך נקודת Z0. או בזמן שהקשת Z Z0 שוה c 31ׂׂׂׂׂׂׂׂׂ)ׂ. והנה ׂבמשולש Z P Z0, שלש צלעותיו ידועות לנו, ולכן נוכל למצא את מדת הנשף או בין השמשות הקצר, שנכנהו tm, על פי משוה זו:
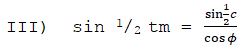
מן המשולש הזה יצא לנו עוד:
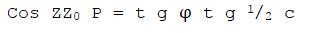
ולפי זה נדע במשולש P S0 Z0, מלבד שתי צלעותיו P Z0, S0 Z0, גם את הזוית P Z0 S0 המתאמת אל הזוית P Z0 Z, ולכן נמצא גם את הצלע P S0, שהיא תשלום נטיית השמש, וממנה גם את נטיית השמש עצמה, שנציינה באות mδ, על פי המשוה הזאת:
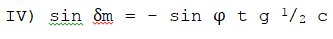
הסימן המשולל מורה, שהנשף או בין השמשות הקצר, נופל אחר תקופת תשרי, בזמן שנטיית השמש היא דרומית.
שיעור הנשף או בין השמשות בתקופת תשרי וניסן, שנכנהו t0, יצא לנו על פי התמונות (II) (I), אם נעשה שם 0 = δ:

אם נקח לנו על כדור הארץ מקום שרחבו φ שוה '30 530 ונעשה בשלש התמונות האחרונות c = 41/40 (שכך יצא לנו שיעור c אם נחשוב בין השמשות בארץ ישראל בתקופת ניסן ותשרי לשליש שעה) אז נמצא שיעור בין השמשות בתקופת תשרי וניסן 7, 28m 37s ובין השמשות הקצר 6, 28m 35s כמו שמצאנו למעלה (צד 17 בהערה), ונטיית השמש בזמן בן השמשות הקצר תהיה 5, 10 42 לדרום, כארבעה ימים וחצי אחר תקופת תשרי (צד 16).
ואם נעשה c = 180, אז נמצא שיעור הנשף ברוחב 531/20 בתקופת תשרי וניסן 2h 5m 12s ושיעור הנשף הקצר 2h 1m 59s כמו שמצאנו למעלה (צד 18) וזמנו בשעה שנטיית השמש היא בערך '19 70 לדרום, או כתשעה עשר יום אחר תקופת תשרי.
על ידי הצורה 2 נוכל להתיר גם את השאלה ההפוכה: למצא על פי ידיעות שיעור הנשף או בין השמשות במקום ידוע בארץ את נטיית השמש δ, ועל ידה את הזמן המכוון לו בימות השנה.
אם את הקשת Z0 Z נציין באות L, את הזוית Z0 S, Z או Z Z0 S2 באות M, ואת הזוית Z Z0 P באות N, הנמצא על ידי שלשת המשולשים: משולש Z P Z0, משולש Z Z0 S, (או (Z Z0 S2 ומשולש Z Z0 P, את שלש התמונות האלה:
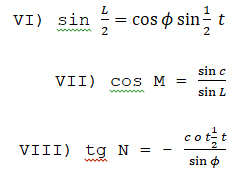
על ידי התמונות (VIII) (VII) נדע את מדת הזוית P Z0 S2 שהוא שוה M – N, או את הזוית P Z0 S, שמדתה (M+N) – 3600 ועל ידי זה נמצא במשולש P Z0 S2 או P Z0 S2 או P Z0 S, את הצלע P S2 או P S, שהיא תשלום נטיית השמש δ, ואת הנטיה δ עצמה על פי התמונה הזאת:

נראה מזה, שבכלל יש להשאלה הזאת שתי התרות: אחת לנטיה הצפונית δ2 או לקשת S2 P, והשנית לנטיה הדרומית δ2 והוא הקשת P S,, אבל אפשר שלא תהיה לה התרה כל עיקר, בזמן אשר במשוה (VII) יצא כי C > L שעל ידי זה Cos M נעשה גדול מן האחדות, (והדבר מובן מאליו, כי אז יצא t <tm , להפך מן ההנחה, כי tm *היא מדת הנשף הקצר, שאין עוד קטן ממנו), וכן בשעה שכל אחד מן המחירים δ, δ2 עובר 30; ואפשר גם כן שאין להשאלה אלא התרה אחת, בזמן שמחיר δ2 הוא קטן מן 231/2 אבל δ1 עובר את השיעור הזה בנטיתו הדרומית.
על פי התמונות האלה נוכל למצוא גם את הזמן, אשר בו ישוב הנשף, או בין השמשות, להיות שוה בשיעורו לכמות שהיה בתקופת תשרי. כי כאשר אמרנו יהיה השיעור האחרון הזה נתון על פי המשוה:
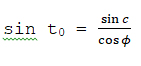
ואם את המחיר היוצא ממנה לשיעור t0 נשוב ונעמיד במקום t בתמונה (VIII) (VI), אז נמצא באחרונה את מדת זוית הנטיה δ. אולם בנידון שלפנינו יש בידינו לקצר עלינו את הדרך, אם נשים אל לב, כי אחד משני המחירים של δ כמו הוא נתון לנו, והוא מחיר δ אשר בתקופת תשרי שהוא שוה 0 או 900 = N – M = 2S P, ומזה נמצא N 2 + 90 = N + M ואם כן יצא לנו המחיר השני:
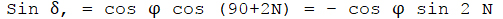
ומחיר N יוצא כיון ממשוה (VIII) מבלי כל צורך להתרת המשויות VI, VII)).
אם נעשה בתמונות האלה c=4.250 , אז יצא לנו שעור δ1 שוה '30 80 ונמצא שבזמן תשעה ימים אחר תקופת תשרי ישוב בין השמשות שנית למחיר שהיה לו ביום התקופה, ואם נעשה c=180, יצא לנו '46 140 = δ, ונמצא לפי זה, שאחר ארבעים יום מתקופת תשרי יהיה הנשף שוה לכמות שהיה ביום התקופה.
נמצאנו למדים (אם נחשוב את הכל לפי חדשי החמה) שהנשף הבינוני שבתקופת תשרי הולך ומתמעט עד י"ט בתשרי, שאז הוא בתכלית קטנו, ומשם הוא מתחיל להוסיף, עד שבעשרה במרחשון הוא חוזר להיות שוה במדתו לכמות שהיה בתקופת תשרי, והולך ומוסיף עד תקופת טבת, שמשם הוא מתחיל להתמעט, עד שבעשרים בשבט הוא שוה לנשף הבינוני, ומוסיף להתמעט עד י"א באדר, שאז הוא פעם שנית בתכלית קטנו, שוה במדתו לכמות שהיה בי"ט בתשרי, ומעתה הוא שוב מתחיל להוסיף, עד שבתקופת ניסן הוא שוה למדתו בתשרי. המשוה את הדברים האלה עם מה שהבאנו למעלה בשם הרב (צד 16), יראה שאין דבריו מדוקדקים היטב.
-————-
על הדבר הזה, שהקצר שבנשפים אינו לא ביום הקצר ולא בעת שווי היום והלילה, כי אם בזמן שבין תקופת תשרי וטבת, ופעם שנית בין תקופת טבת וניסן – עמד כבר עוד באמצע המאה השש עשרה החכם פדרו נונוס (Pedro Nunez), שהביא את השאלה הזאת במשפט. החכם הזה, שהיה מורה בבית המדרש הגדול בפורטוגליה (נולד בשנת 1492, היא שנת גירוש היהודים מספרד ומת בשנת 1577) חי בראשית ימי תחית המדעים באירופה, בזמן שהחכמות הלמודיות בכלל וחשבונות המשולשים בפרט, עמדו עוד בשפל המדרגה (כאשר נראה מספרו של קופרניקוס על חשבונות המשולשים), ובכל זאת הצליח להתיר כמה שאלות קשות ומסובכות, שאלותיו ותשובותיו יוצאות מגדר הרגיל, ומצטיינות תמיד בעומקן ובחריפותן. הוא הוא אשר נתן לבבו להתחקות על מהלך הצל המושלך על ידי נקודה חומרית התלויה באויר ונופל על פני הארץ, ומצא שהקו העקום הנולד על ידי התנועה הזאת יהיה הקו ההיפרבולי, והוכיח, כי בתנאים מיוחדים יוכל הצל לשוב אחורנית. הוא גלה עוד בטרם נתחדשה המדידה האנליטית על ידי דיקרט וחשבון הנשגב על ידי ניוטון וליבניץ – את הדרך אשר תעשה נקודה המתנועעה על פני כדור הארץ, אם בכל עת מהלכה תשמור לעשות עם כל קוי הצהרים שהיא עוברת עליהם, זוית קבועה וקיימת במדתה. הקו הזה, שהוא בעל עקמומית כפולה, הוא הקו הלוכסודרומי, אשר על פיהו יצאו ויבואו עתה כל האניות הגדולות, המפליגות בים האקינוס. הוא השכיל למצוא גוף הנדסי מורכב מחלקים הרבה מתמונות שונות אשר יוכל להרשם בכדור ולמלאותו, שאין פה המקום לדבר עליו, הדבר הזה אין לו כל תועלת מעשית אבל מורה כמה היה כחו גדול בכל מקצעות חכמת השיעור ועד כמה היה נוטה מטבעו להעמיק מחשבה. הוא תקן תקונים רבים בכלי המדידה המשמשים בחכמת ההנדסה והתכונה (ויש מיחסים לו גם את הכלי הידוע בשם Nomius, אבל אין הדבר ברור). הקוראים אולי יתפלאו, כי נטיתי מדרכי והכנסתי עצמי בדברים שמקומם בספרי קורות המדעים, אולם ידעו נא כי האדם הגדול הזה ממעי יהודה יצא (“איש גדול בלמודים מזרע היהודים”, כדבר יש"ר מקנדיא, חקות שמים, שאלה ל"ה), אחד מהמון האנוסים אשר העבירה הכנסיה הקטולית באהבתה ובחמלתה על דעתם ועל דעת קונם. סופרי דברי ימי היהודים לא יזכירו את שם החכם הזה בספריהם (אולי בגלל עזבו אמונת ישראל, או אולי בעבור שאין רובם בקיאים בקורות חכמת ההנדסה). ולכן אמרתי להקדיש פה דברים מעטים לאדם הנעלה הזה, אשר חריפתו הגדולה אולי מורשה היתה לו מאבותיו המעמיקים בתורה, ואשר לולא נטרפה עליו השעה, בלי ספק היה לעמו לגאון, לצבי ולתפארת.
-————
אלו הם הדברים שיש בהם צורך להבנת דברי הרב בענין בין השמשות. אולם בדבר ההטיה כלפי ירושלים יספיקו לנו לגמרי שתי התמונות שהבאתי בהערות במקומן (צד 6, 11). אבל בכל זאת רואה אני לתת בזה שני לוחות קטנים, שערך ידידי הרה"ח ר' צבי יפה. הראשון יכיל את כל המקומות שיושביהם צריכים לעמוד מכוון כלפי אמצע המזרח, והשני את כל המקומות שיושביהם צריכים להטות מאמצע הדרום כלפי מזרח שלשים מעלות. שני הלוחות ערוכים לפי רוחב המקומות ממעלה למעלה מל"ב עד ס"ו מעלות.
לוח א.
| אורך מערבי | רוחב צפוני | אורך מערבי | רוחב צפוני | אורך מערבי | רוחב צפוני | אורך מערבי | רוחב צפוני |
|---|---|---|---|---|---|---|---|
| 8 | 59 | 39 | 50 | 30 | 41 | 12 | 32 |
| 68 | - | 58 | - | 44 | - 7 | - | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 2 | 60 | 52 | 51 | 29 | 42 | 20 | 33 |
| 69 | - | 59 | - | 46 | - | 17 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 54 | 61 | 2 | 52 | 20 | 43 | 12 | 34 |
| 69 | - | 61 | - | 48 | - | 23 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 45 | 62 | 9 | 53 | 4 | 44 | 42 | 35 |
| 70 | - | 62 | - | 50 | - | 27 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 35 | 63 | 14 | 54 | 41 | 45 | 26 | 36 |
| 71 | - | 63 | - | 51 | - | 31 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 24 | 64 | 16 | 55 | 13 | 46 | 39 | 37 |
| 72 | - | 64 | - | 53 | - | 34 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 12 | 65 | 17 | 56 | 41 | 47 | 29 | 38 |
| 73 | - | 65 | - | 54 | - | 37 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 59 | 66 | 16 | 57 | 4 | 48 | 3 | 39 |
| 73 | - | 66 | - | 56 | - | 40 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| - | - | 12 | 58 | 23 | 49 | 22 | 40 |
| - | - | 67 | - | 57 | - | 42 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
לוח ב.
| אורך מערבי | רוחב צפוני | אורך מערבי | רוחב צפוני | אורך מערבי | רוחב צפוני | אורך מערבי | רוחב צפוני |
|---|---|---|---|---|---|---|---|
| 49 | 59 | 43 | 50 | 7 | 41 | 8 | 32 |
| 16 | - | 11 | - | 6 | - | 0 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 21 | 60 | 19 | 51 | 45 6 | 42 | 49 | 33 |
| 17 | - | 12 | - | - | - | 0 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 54 | 61 | 54 | 52 | 24 | 43 | 29 | 34 |
| 17 | - | 12 | - | 7 | - | 1 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 24 | 62 | 28 | 53 | 2 | 44 | 10 | 35 |
| 18 | - | 13 | - | 8 | - | 2 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 55 | 63 | 3 | 54 | 39 | 45 | 50 | 36 |
| 18 | - | 14 | - | 8 | - | 2 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 25 | 64 | 37 | 55 | 28 | 46 | 30 | 37 |
| 19 | - | 14 | - | 9 | - | 3 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 55 | 65 | 10 | 56 | 54 | 47 | 9 | 38 |
| 19 | - | 15 | - | 9 | - | 4 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| 25 | 66 | 44 | 57 | 30 10 | 48 | 49 | 39 |
| 20 | - | 15 | - | 10 | - | 4 | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
| - | - | 17 | 58 | 7 | 49 | 28 5 | 40 |
| - | - | 16 | - | 11 | - | - | - |
| ===== | ====== | ====== | ===== | ===== | ===== | ==== | === |
אם נצרף את כל המקומות שבלוחות לפי מצבם על פני הארץ אז יצא לנו מן הלוחה ראשון קו עקום העובר מירושלים דרך הים התיכון ונכנס לאספמיה סמוך לקרתגא ועובר דרך מורסיה וקסטיליה החדשה עד סמוך לפורטינה, ומשם נכנס לארץ פורטוגליה, ועובר אותה לרחבה, ויוצא משם סמוך למורטוזה אל הים האטלנטי, (ורוב ערי מושב היהודים באנדילוזיה אשר בספרד, כגרנדה סיבליה ועוד, וכן ליסבון ורוב ערי פורטוגליה נמצאות לדרומו של הקו הזה, והיושבים שם בפנותם לירושלים, צריכים לנטות מעט מאמצע המזרח כלפי צפון, אעפ"י שרחבו לצפון המשוה גדול יותר מרוחב ירושלים.
הקו העקום היוצא מן הלוח השני עובר מירושלים דרך הים התיכון והמרמורי לקונסטנטינופול, ומשם עובר דרך הים השחור ויוצא בין ווארנא לשומלא והולך דרך בוקרשט ולבוב וחולף דרך ערי פולין: לובלין, ווארשא לקניגסברג; (ובשום אופן אינו מתאים למקום מושב הרב בלאדי, שבהיות רחבה לצפון המשוה '45 540 וארכה למערבה של ירושלים '20 40, צריכה שם זוית הנטיה להיות יותר מן 800).
אנסה עתה לתת להמעיין מושג מעט מן המספר A הזה. החקירות האחרונות של חכמי הטבע הוכייחו, כי בכל ליטר מלא חומר אוירי (שחומו הוא 00 וכח לחיצתו m m760), ימצאו פרודות בשיעור 71 x 1022 (מספר גדול קרוב לארבעים אלף פעמים ממספר גרעיני החטים שבס"ד משבצות שאמרנו). ואם נצייר לנו בדמיוננו כדור גדול ונורא, של חומר אוירי כזה, שמספר פרידותיו ישוה למספר הציונים, שאנו צריכים לכתיבת המספר A על פי שיטת העשיריות הנהוגה בינינו, הנה יצא לנו שהזמן שיצטרך האור במהירותו העצומה, (העולה עד 300000 קיטלומטר לסיקונדה) לעבור את הכדור הזה משפתו אל שפתו יעלה יותר משיעור 294 x 1024 או 294 קוואדריליון (לפי מובן השם הזה אצל האשכנזים) שנות החמה בנות שס"ה יום ורביע, ומפני שכתיבת כל אחד מן הציונים האלה דורשת רבוא רבבות פרודות של דיו, הנה נצטרך לכתיבת המספר A רבוא רבבות כאלה מן השחור השחור הזה.
-
החכם מימון בספר תולדותיו יאמר בעצמו, כי את ראשית למודיו קנה מספרים הכתובים עברית, ואת חכמת התכונה– מן הספר נחמד ונעים (Salonon Mainon’s Lebensgeschichte I, 38, 39, והצורה שהוא מזכיר במרוצת דבריו, היא אותה שבספר נחמד ונעים סימן ל"ב), עד אשר מצא אחרי כן ביד רב אחד מעיר הרחוקה ממנו כששים פרסאות, שהיה מתגורר לפנים בארץ אשכנז, מקצת ספרי-חכמה כתובים בשפה ההיא )שם צד 144), וככה יאמר על הרב בעל נצח ישראל, שהוא שאב את חכמתו מספרים עברים (שם 169). כי מלבד המכשולים אשר מצאו רודפי המדע מצד אחיהם הקנאים, הנה גם עין הנוצרים היתה צרה בהם, ולא רצו ללמדם שפת רומית ופולניא (שם צד 121). והדעת נותנת כי גם ר' ברוך משקלוב רכש לו את ידיעותיו הראשונות מספרים עברים, כמו מספר “אלים” שהוא מזכירו בספרו “עמודי שמים” (דף ט"ז), וכפי הנראה משם לקח את לוחות הבקעים, שהדפיס בסוף ספרו זה (אכן אחר כך כבואו אל ארץ אשכנז רכש לו לשונות אחרות, וספרו “קנה המדה” העתיק משפת אנגלית), ונקל להוציא משפט כי גם הגר"א שאב את כל חכמתו וידיעתו מספרים עברים, וכפי אשר יעידו עליו בניו בהקדמתם לספרו “אדרת אליהו”, “היה מעיין בספר תכונת השמים”. בשם הזה ידוע לנו אך ספר אחד שחבר ר' רפאל הנובר (ולפי זה הפריזו בניו מאד על המדה באמרם שהיה אז בן שמונה או י"ב שנה, כי הספר הזה, לא נדפס עד שנת תקט"ז, והיה אז הגר"א לא פחות מל"ו שנה, אם לא נאמר כי טעות נפלה בדבריהם, וצריך להיות בספרי תכונת השמים, המורה בכלל על ספרים המדברים על דבר חכמת התכונה). אבל יתר מזה נראה כי שאב הגר"א את ידיעותיו גם מספר “שבילי הרקיע”, שנדפס בראשונה בשנת תקמ"ה. כי את הקו הידוע בחשבון המשולשים בשם Cosinus יקרא בספרו “איל משולש” בשם"תשלום בקע", בעת אשר כל חכמי ישראל שקדמוהו קראוהו בשם “בקע תשלום”. כן יכנוהו בעל ספר “אלים” ובעל “עמודי שמים” ו"קנה המדה", כי כן היה נקרא לפנים גם בלשונות העמים Sinus complementi (וכן כתבה באותיות רומיות בעל “קנה המדה” בספרו דף ה') שפירושו: בקע תשלום, כלומר הבקע של הקשת המשלמת אל צ' מעלות, והראשון אשר הפך את הסדר וכתב תשלום בקע הוא בעל “שבילי דרקיע” שהלך בעקבות החכמים האחרונים שכנו את הקו בשם Cosinus ואחריו נמשך גם הגר"א, ולפי זה כתב הגר"א את ספרו “איל משולש” לעת זקנתו. ועל אודות המקורים שמהם שאב הרב, עיין להלן (עמוד 10 ובהערה 2 שם). ↩︎
-
בדפוס מתחיל המאמר המוסגר ממלת “קצת”, וטעות הוא, וכן כתוב שם “במשולש סדורי” במקום “כדורי”. ↩︎
-
אם נכנה את רחב המקום ϕ ואת מרחקו למערבה של ירושלים θ, אז נמצא את מדת הקשת המתבקשת על ידי המשוה Tgx=cos θ tg ϕ ולפי ערך השעור cos θ tg ϕ, אם הוא גדול או קטן מן 0,62003 שהוא הנוגע של '48 310 (רחב ירושלים), צריכים יושבי המקום להדרים או להצפין. ↩︎
-
לפי גבולות ארץ רוסיא בסוף ימי הרב (אחר חלוקת פולין השלישית שהיתה בשנת תקנ"ה), היו הערים הנוטות ביותר לרוח צפונית מערבית: בריסק-דליטא –’5 520 לצפון המשוה, '44 110 למערב ירושלים, ופאלאנגען –’30 560 לצפון, '45 130 למערב; ועל פי החשבון נמצא, שיושבי הערים האלה בפנותם נוכח ירושלים צריכים לנטות מאמצע הדרום כלפי מזרח: בראשונה '27 270, כבשניה '56 260, וחסר אפוא לשעור שנתן הרב יותר משתי מעלות וחצי. ↩︎
-
קציבת המקומות על פני כדור הארץ ביבשה ובימים לפי ארכם ורחבם אינה נעשית – כפי שיבין כל איש מעצמו – על ידי מדידה בחבל בפועל ממש, כי אם על ידי השקפות וחשבונות מיוסדים על חכמת התכונה. הקלה שבמדידות כאלו היא קציבת רוחב המקום, הנעשית על ידי מדידת גבהו של כוכב הציר, (אף שגם היא צריכה עוד לתקונים, מפני שהכוכב אינו עומד על מקום הציר ממש ומפני שקרני האור נשברים באויר, ומפני שאין צורת הארץ ככדור הנדסי מדוקדק, וקו האור העושה זוית נצבת עם האופק אינו נופל מנקודת מרכזה של הארץ). אבל קשה ממנה הרבה היא קציבת אורך המקומות היוצאת רק מתוך הבדל הזמן שבין שני מקומות. הדבר הזה, שהוא לנו עתה, בזמן שחוטי הטלגרף מתוחים על פני כל הארץ, “כמשחל ביניתא מחלבא”, כמעט שהיה נמנע אצל הקדמונים. בעל האלים יאמר על זה (תמר נ"ג), שהוא “מן הדברים היקרים”, “ושרי המדינות נדרו מתנות גדולות למצא אופן ולמוד על זה, ויגעו ולא מצאו”. “הרבה בקשו למצא זה על ידי כלי-החול (ראוי להוסיף “והמים”, זאנד אונד וואַססעֶראוּהרעָן), אבל “אין הכלים האלו מתנועעים בשווה, שבתחלתם (שגובה המים בכלי גדול יותר) הם מהירים, ובסופם (כשהוא פוחת והולך) חלושים”. ויש”ר מגלה לשואלו רז שקבל מפי אחדמחובלי הים “בקי ומובהק” במלאכתו, על דבר תחבולה אחת (שבאמת השתמשו בה עוד היונים והרומיים הקדמונים בכלי-שעות של מים שהיו נהוגים אצלם, עיין גינצל, כרונולוגיה ןן, 305), שכל עיקרה הוא לשמור את המים בכלי הזכוכית, שישארו תמיד בגובה אחד קיים וקבוע, על ידי הוספת מים חדשים כשיעור היוצאים, ומתוך כך הרקת המים נעשית תמיד במדה אחת, והוא מוסיף: “עם כל זה הכלי הזה קשה השמוש”, “וידעתי חכם חשוב בלמודים מאי אנגליאה, שיש לו כלי מתמיד שלשה חדשים בתנועתו ומכוון עם תנועת השמים, ואינו רוצה לגלותו אם לא שיתנו לו ראשי העיר ממון רב”.מן הדברים האלה נראה, כמה היתה קציבת ארכי המקומות רחוקה מן הדיוק אצל הקדמונים, ועד כמה גסים היו הכלים, שהשתמשו בהם חובלי הים עוד בימי יש"ר, במחצית הראשונה למאההשבע עשרה למנין הרגיל. השאלה הנכבדה הזאת, שהרבתה להעסיק כל כך את בעל האלים, לא הותרה כי אם כשלשים שנה אחרי כן על ידי החכם המפואר Huyghens, שתיקן בשנת 1656 את האורולוגין של כיס על ידי שערה דקה של מתכת מגוללה בתמונת חלזון (שגעֶקקעֶנפאֶרמינע פעֶדער), המשמשת כידוע גם היום ליַשר את תנועתם כראוי. האורלוגין האלה הַנִשָׂאִים בחיל ממקום למקום, נתנו את היכולת בידי חובלי הים לדקדק יותר בקציבת המקומות. אבל אל הדיוק המוחלט לא הגיעו, כי אם אחר התגלות הטלגרף, שעל ידו נוכל לדעת בכל זמן את שעות היום ורגעיהן במקומות השונים אשר בכדור הארץ, ולקצוב על ידי הבדל הזמן את הבדל האורךשביניהם. אחרי הדברים האלה לא יפלא בעינינו מדי נתבונן על ארכי המקומות, שאסף התוכן תלמי בגיאוגרפיה שלו, אם הם רחוקים הרבה מן האמת. התוכנים הערביים שבאו אחריו דקדקו יותר ממנו, בכל זאת גם בידיהם לא עלה הדבר כראוי, וגם יוצר התכונה החדשה, קופרניקוס, עודנו תועה בקציבת ארכי המקומות (עיין בהקדמת המו"ל את ספרו De revolutionibus orbium coelestium, דפוס ווארשא שנת 1854 צד XXXIX). אבל הדבר המתמיה ביותר הוא, כי בעל ספר אלים, שכתב ספרו קרוב למאה שנים אחר הופעת ספרו של קופרניקוס, נוטה יותר ממנו מן האמת בקציבת ארכי המקומות. מרחק עיר קראקוי מאלכסנדריא של מצרים שהוא באמת '55 90 נקצב אצל קופרניקוס בשיעור 150, ואצל יש"ר '50 170. מרחק קראקוי מרודוס, שהוא באמת '16 80, הוא אצל קופרניקוס '30 120 ואצל יש"ר '20 150. מרחק קראקוי מרומא, שהוא באמת '31 70, אצל קופרניקוס 50 ואצל יש"ר '10 60. אם במשל האחרון מחירי יש"ר מדוקדקים יותר משעוריו של קופרניקוס, הנה לעומת זה בשני המשלים הראשונים נופלים הם ממנו בדיוקם הרבה יותר. ↩︎
-
את העיר באיונה לקח לו בעל “נצח ישראל” למשל להוכיח על ידה, כי גם בארצות שהן צפוניות לארץ ישראל, נצטרך לפעמים להטות כלפי צפון, כאשר נראה לפנינו להלן (עמ' 12 בהערה), ולכן יש מקום לבעל דין לחשוב גם הפעם, כי החלטת הרב על דבר מקור המנהג לעמוד בתפלה למזרח, לא יצאה לו מחשבונו, כי אם מדברי בעל “נצח ישראל”, כי שיעור הנטיה לפי המספרים שתפס שם אינו עולה גם לשתי מעלות, והמקומות הצפוניים לה יש מהם שצריכים לעמוד במכוון כנגד המזרח. אולם שיעור הנטיה שנתן הרב בעל התניא למדינת רוסיא, מוכיח בבירור גמור, כי עשה בעצמו את חשבונותיו, וכי סמך בהם על לוחות יש"ר. ↩︎
-
מרשימת הספרים שהיו בידי הרב (עיין למעלה ח"ב צד 247–246) נראה, כי מלבד ספר האלים עוד היו בידו ספר תכונת השמים לר' רפאל הנובר (אמשטרדם תקט"ז) וספר יסוד עולם להישראלי (ברלין תקל"ז). שלשת הספרים האלה היו לפי זה כל המקורים אשר מהם שאב הרב את ידיעותיו בחכמות הלמודיות. ↩︎
-
בכל משולש כדורי ששתי צלעותיו b, a והזוית C הסגורה ביניהם ידועות לנו, נוכל למצוא את קבוצת שתי הזויות האחרות A+B, ואת יתרונן A-B, ועל ידיהם גם את כל אחת מן הזויות A, B, על פי התמונות האלה: ↩︎
-
ספר “אמונת חכמים נדפס, כפי ידיעתי, חמש פעמים: ראשונה במנטובה (שנת ת"צ). אחרי כן בזלקאווע (תר"ח). בלבוב (תרי"ח). ורשה (תרמ"ט) ובאאנניסבורג בלי שנת הדפוס P בערך שנת תרכ”ה). הוצאות זלקאווע, לבוב וורשה נעשו זו מתוך זו, ויש בהן טעיות לרוב, והוצאת יאהנניסבורג, שלא מצאתי לרושמי הספרים שיזכירוה, נעשתה לפי דפים מנטובה (ובטעות נאמר בשער הספר: “נספס מקדם בפאדוא שנת תפ”ט) ומדויקת ביותר. המאמר האיטלקי, שרמז עליו המחבר בפנים ספרו (באמצע פרק כ"ד, והוא בדפוס מנטובה דף מ' ע"ב, ובדפוס יהאההינסבורג דף מ"ו ע"ב) באמרו: “ובסוף הספר אבאר הכל בלשון לעז”, נמצא באמת בדפוס מנטובה בסופו (עיין ראזענטהאל “יודע ספר” צד 26). אבל בדפוס יאהנניסבורג נמצא בתחילתו, וביתר ההוצאות השמיטוהו המדפיסים לגמרי. ↩︎
-
בעל אמונת חכמים הראה זאת במשל על העיר ליסבונה, שרחבה הצפוני לפי דבריו '38 390 גדול מרחבה של ירושלים (שהיא אצלו 320), אבל מפני שהיא למערב ירושלים בשיעור '20 540 (כי אורך ירושלים לדבריו '30 630 ואורך ליסבונה '31 90). יושביה צריכים להטות כלפי צפון בשיעור '31 70. דרך התרתו כאשר אמרנו הוא יפה ונכון, אבל תוצאות חשבונו אינן מדוקדקות, מפני שבאמת אין ההבדל שבין ירושלים וליסבונה עולה כי אם '20 440 ורוחב ליסבונה הוא “24 '42 380, ואם כן אין זוית הנטיה לצפון עולה כי אם 3 מעלות בקירוב גדול. אולם אם אצל הרב בעל אמונת חכמים הוליד חסרון הדיוק באורך המקומות ורחבם רק הבדל במדת הנטיה אבל לא בעיקר החלטתו שבליסבונה צריכים לצדד לצפון, הנה לא כן הדבר עם בעל “נצח ישראל”, כי הטעותבקציבת המקומות שהביא לו למשל: טוליטולה ובאיונה, שמו לאל את כל חשבונותיו והוכחותיו. על פי הלוחות שהיו בידו קצב את ההבדל שבין ירושלים וטוליטילהבאורך לשיעור 560 בזמן שבאמת ההבדל שלה עולה רק “45 '10 390 (רוחב טוליטולה שהוא אצלו 400 אינו נבדל מן האמת כי אם בשיעור קטן, כי רחבה הוא "24 '52 390), וכן קצב את ההבדל באורך בין ירושלים ובאיונה 490, בזמן שההבדל האמתי הוא אך “12 '40 360 (וגם הרוחב שקצבו 420 אינו מדוקדק אצלו היטב כי באמת מדתו "29 '29 430). ולכן צריכים יושבי המקומות ההם להטות באמת כלפי הדרום בראשונה '55 10 ובשניה '43 90 ולא לצפון כאשר יצא לו בחשבונותיו.וראוי להעיר עוד, כי מקומה של טוליטולה, כפי שקצבו בעל “נצח ישראל”הוא מכוון בדקדוק עם מה שקצב יש”ר מקנדיאה “בחקות שמים”, אבל מקומה ורחבה '50 420. וקרוב הדבר מאד בעיני שבעל “נצח ישראל” עזב בכוונה את מספר הדקים שבאורך ורוחב, כדי שיוכל להביא ראיה לדבריו לא רק מארץ ספרד לבד, כי גם מארץ צרפת, כי אלו לקח את המספרים כמו שהם אצל יש”ר, כי אזיצא לו, כי יושבי באיונה צריכים לצדד קצת כלפי דרום, להפך ממה שהחליט שהם צריכים להטות כלפי צפון, אבל ההטיה הזאת לדרום מועטת היא מאד, ואינה עולה כי אם חלק אחד מי”ב במעלה. ↩︎
-
עיין מה שכתבתי בענין הזה במאמרי בין השמשות" בהאסיף (שנת תרמ"ח) ומאמר “ספק חשכה” (האסיף שנת תרמ"ו). ↩︎
-
השיעור הזה מכוון עם השיעור שקצב הרמב"ם (הלכות קידוש החודש פרק י"ד הלכה ו') לזמן ראיית הלבנה החדשה בתחילת החודש, כי אור הלבנה בתחילת הראותה כחו ככח אורם של ככבים בינונים. ↩︎
-
גם הגר"א יאמר כי השיעור בין השמשות שבתלמוד הוא מיוסד על ניסן
ותשרי, אבל ראוי להעיר כי בארץ ישראל שיעור בין השמשות בתקופות טבת ותמוז אינו נבדל הרבה מבין השמשות הבינוני, כי בטבת יעלה 221/3 ובתמוז 23, הבדל שאינו מורגש כלל לעינים. ↩︎
-
וז"ל הרב בסידורו, עד כמה שהוא נצרך לענינינו: “צריך ליזהר בהדלקת נרות להדליק קודם שקה”ח שקיעה הנראית, דהיינו בעוד השמש זורח בראשי האילנות בשדה בארץ המישור, או בראשי גגים הגבוהים בעיר וכו' כדי להוסיף מחול על הקודש מעט, כי אחר סילוק וביאת האור מראשי האילנות וגגים הגבוהים בכמו ד' חלקי ששיים משעה, אזי היא שקיעה האמיתית שהוא סילוק וביאת האור מראשי ההרים הגבוהים שבא"י, ואז הוא תחילת זמן ביה"ש וכו', כי בשליש שעה משעות השוות אחר שקיעה האמיתית הוא ודאי לילה בא"י בימים השוים, שאז הוא זמן צאת ג' כוכבים בינונים בא"י בימים אלו, וגם בכל החורף כמעט כו' ובמדינות אלו זמן צאת ג' ככבים בינונים בימים השוים הוא בכמו חצי שעה בקירוב אחר שקיעה האמתית, שהן ל"ד חלקי ששיים בקירוב אחר שקיעה הנראית וכו', וכן בכל החורף כמעט, שבמרחשון של חדשי החמה פוחת מעט מתשרי, שנראית אז ג' כוכבים בכחצי שעה אחר שקיעה הנראית, ובטבת עודף מעט על תשרי ובאדר חוזר ופוחת מעט כבמרחשון, ובניסןחוזר להיות בשוה עם תשרי. עי' בס' אילים במעין התום" עכ"ל. ↩︎
-
מפני שבתקופת תשרי השמש מהלכת על עגול המשוה העושה עם עגול האופק זוית השוה במדתה לתשלום רוחב המקום, לכן אם ברגע סוף ביה"ש נמשך ממרכז השמש קשת נצבת על עיגול האופק, אז תעשה הקשת הזאת עם קשתות האופק והמשוה משולש נצב, אשר מלבד הקשת הזאת שנכנה אותה בשם c, נדע בו גם אתהזוית שכנגדה שהיא φ – 900, ולכן נמצאו גם את קשת המשוההמודדת את הזמן שאחר שקה"ח, שנציינה באות t על פי המשוה sin t = sin c מחולק ל cos-φ ↩︎
-
ידיעת שיעור ביה"ש, שלא בימים השוים, דורשת מאתנו התרת שני משולשים כדוריים (האחד לזמן השקיעה והשני לגמר זמן ביה"ש), שאנו צריכים למצא בכל אחד מהם אחת מזויותיו עפ"י ידיעת שלשת צלעותיו, התרת השאלה הזאת קלה מאוד ויוצאת כיון עפ"י התמונה (II) המובאה בחתימת המאמר, ואםלא נשים לב לשבירת קרני האור (כאשר עשה כן בלי ספק הרב), אז יקל לנו הדבר עוד יותר, כי בהתרת המשולש הראשון נוכל להשתמש בתמונה (ו) הפשוטה יותר. אבל להרב, ששאב את כל ידיעותיו רב מספר אלים, שהתרת המשולשים העקומים נפתרת שם רק על ידי הפיכת המשולש העקום למשולשים נצבים, היו דרכי החשבון קשים ומסובכים ביותר, וכאשר נראה ממה שנתלבט בהם היש"ר בעצמו בפנה השלישית מספר “סוד היסוד” אבן ג' טור ו', המתואר אצלו בשם “צדייתאחת משלש זויות מידיעת שלשת הצלעות”, וכן ממה שלא היה בידו לפתור שאלהדומה לזו ששאל אותו עלי בן רחמדן המצרי “לדעת כמות הצלעות מבלי הפוך אל המשולשים נצבי הזויות” (הפנה השנית מספר “סוד היסוד”, סימן ס,ג) והוזקק להתירה על ידי הורדת עמודים נצבים (שם בפנה השלישית הטור י"ב). ↩︎
-
אם נניח סוף הנשף בשעה שהשמש היא י"ח מעלות תחת האופק, אזיהיה ברוחב 531/20 סוף שיעור הנשף בתקופת תשרי "12 m5 h2 והנשף הקצר "59 m1 h2 וההבדל שביניהם "13 m3. ↩︎
-
נקל להוכיח כי אם נציין חצי קוטר השמש באות R ואת זוית חלוף המראה שלה באות η, ואם נקח את חצי קוטר הארץ למדת האחרות ואת חצי קוטר כשמש הנראה במדתה הבינונית 2,‘16, אז תצא לנו משוה כזאת Π; 16,2 = R אם נשים במקום η את מחירו 95,"8 שעלה בידי התוכנים האחרונים, אז יצא לנו חצי קוטר השמש R שוה 6,’108 בחצי קוטר הארץ. אבל לפי דעת הרב שקוטר השמש שהוא R 2 הוא י"א אלפים פרסאות שהוא 6,4 פעמים בקוטר הארץ, אז יצא לנו זוית חלוף המראה 5,'2=Π הגורם הבדל בשקיעה רק בעשר סקונדין. ↩︎
-
וז"ל החכם יש"ר (“חקות שמים” שאלה ל"ה): “ואולם אודיעך שהתחלת הנשף לא תהיה בפחות משקיעת השמש תחת האופק ט”ו מעלות בערב, וכן סופו בבקר וסופו לא יותר מי"ח מעלות בערב, וכן התחלתו בבקר ולדעת קצת עד כ' מעלות שקיעה יהיה עדין נשף". ↩︎
-
כארבע שנים אחרי שנדפסו דברי יש"ר, נתפס החכם גליליאוס (שהיש"ר בספר “אלים” מכנהו בשם רבו ומורו) על הסבירו פנים לשיטת קופרניקוס, והועלה לגרדום לידון לפני בית-דין הקדוש אשר ברומה בשנת 1633, וכל עמל אוהביו ומעריציו, שהיו מחורי העם וסגניו, לא הועיל להצילו מרעתו, לולא נכנע והתודה לפני משופטיו על משוגתו וקבל על נפשו באלה ובשבועה לבלתי ישוב עוד לכסלה. (נקל להבין, כי היה הזקן האמלל נשבע בשפתיו ומבטל בלבו, ומהרהר במחשבתו: E pur se muove – “ובכל זאת נוע תנוע”. אולם זה שיאמרו עליו כי קרא את הפתגם הזה לפני השופטים בקול, וכי בעט בקרקע לאחר שבועתו, אינו יוצא מכלל אגדה). ↩︎
-
מושג כזה על דבר מראות הצבעים היה גם להמגיד ממיזריטש. הוא כותב: “ידוע שכל דבר בשורשו הוא לבן ותחלת תולדתו היה לבן” (אור תורה, שיר השירים, ד"ה: כחוט השני שפתותיך). ↩︎
-
ראוי להעיר, כי הרב, אם אמנם כאשר ראינו, זרה היתה לו תורת הצבעים, היטיב בכל זאת לראות, כי גוון התכלת, שבני אדם רגילים ליחסו לרקיע אינו אלא מראה האויר. והוא אומר: “גוון התכלת הנראה לעינינו הוא מראה האויר, ולא מראה השמים” (לקוטי תורה, נצבים). אך כמובן בא הרב להחלטה זו לא מתוך חקירותיו על טבע האור, כי אם על ידי הנחתו ש"שמים הוא בחינת מקיף עליון כמו שמים לרום שאינו נראה על הארץ" (עיין שם). ↩︎
-
וזה לשון הרמב"ן בפירושו לתורה (בראשית ט', י"ב): “ואנחנו על כרחנו נאמין לדברי היונים, שמלהט השמש באויר הלח יהיה הקשת בתולדה”. ↩︎
-
השם איתיר נתקבל זה כבר בספרותנו, בעברו מלשון יונית דרך שפת ערב אל לשון הקודש. אבל אלו חפצנו לחדש בעבורו מלה עברית, כי עתה אמרתי לכנותו בשם זהריר השוה במשמעותו לשם איתיר שהוראתו ביונית מאיר. ↩︎
-
ובזה דברי הרב קרובים להיות דומים לאמונת האסטרולוגיה, המיחסת לכל אחד מכוכבי השמים פעולות ידועות בארץ, וקוצבת לכל אחד מהם מקום מיוחד. אף שאין ביניהם כל ערך בבחינת שטח מקום. ↩︎
-
מדה זו להראות את טעותם של חכמי הטבע והחוקרים נמצאת גם אצל גדולי החסידים כהבאש"ט ור"ג מברסלוב, ביחוד נהג זה האחרון קלות-ראש בהחוקרים (עיין בפנים הספר ח"א עמ' 19 הערה 1). ↩︎
-
כספר תכונת השמים (שהיה ביד הרב, כאמור למעלה), שיחד לדבר הזה סימן מיוחד להוכיח, כי “הארץ היא כנקודה בתוך הגלגל” (עיין שם סי' ט"ז). ↩︎
-
הרב בחר לו לדוגמא המספר “י' רבבות”, אבל לפי שאין למספר עשר רבוא שם מיוחד בלשון, חשבתי לנכון להשתמש במקומו במלת “רבוא”, הכל הוא ענין אחד. ↩︎
-
אחד מן החכמים בדורות האחרונים ברא לו עוד מספר גדול הרבה יותר, ההגוי רק בארבע אותיות, שכל אחת מהן שוה למספר ארבעה, וכל אחת נעשית מדרגה לחברתה הנמוכה ממנה, המספר הזה אשר נציינהו באות A יכתב כזה: ואם נערוך אותו למספריו של ארכימדס, יהיה גדול יותר מתקופת התשע עשרה. והנה נקל להראות, כי המגביל (לאֶגאַריטהמוס) של המספר A הזה יהיה a x 2515, וכל איש אשר יזכיר לנפשו את מקרה האיש, אשר דמה למלאות את ס"ד משבצות הלוח של שחוק האישקקי גרעיני חטים, שברל אחד מן המשבצות יהיה כפלים מן הקודמת לה, יכיר מיד כי יש לו פה עסק עם מספר גדול ועצום ממנו הרבה יותר בלי ערך, כי שם המספר 2 עולה למדרגה 64 ופה למדרגה 512, ועל אחת כמה וכמה המספר A, שהמספר הזה הוא מגביל לו. בכל זאת אשתדל להסבירו מעט לקורא המבין. המגביל A יוכל להכתב עודו בתמונה אחרת a X 10256a או 8072x10150, אשר כפי שיטת המספר שלנו יהיו בו 154 ציונים. נמצאנו למדים שהמספר A אלו אמרנו לכתבו בדרך הנהוג, היה דורש ממנו המון ציונים, שמספרם עולה למספר 10 מורם למדרגה שציוניה עולה 154. ↩︎
- בהאסיף נפלה טעות וצ"ל כמו שכתוב כאן. ↩︎
-
באופן הראשון ZZ0 = ZS0 – Z0 S0 = c; —אבל בשני האופנים האחרים Z S < Z Z0 + Z0 S1—- וכן Z S2 + Z0 Z > S2 Z———או Z Z0 + 90 > 90 c ומזה ZZ0 > c ואם כן בשני האופנים האלה הקשת L גדולה ממה שהיא באופן הראשון. ↩︎
מהו פרויקט בן־יהודה?
פרויקט בן־יהודה הוא מיזם התנדבותי היוצר מהדורות אלקטרוניות של נכסי הספרות העברית. הפרויקט, שהוקם ב־1999, מנגיש לציבור – חינם וללא פרסומות – יצירות שעליהן פקעו הזכויות זה כבר, או שעבורן ניתנה רשות פרסום, ובונה ספרייה דיגיטלית של יצירה עברית לסוגיה: פרוזה, שירה, מאמרים ומסות, מְשלים, זכרונות ומכתבים, עיון, תרגום, ומילונים.
ליצירה זו טרם הוצעו תגיות
אין עדיין קישוריות מאושרות

